A variance principle explains why dropout finds flatter minima

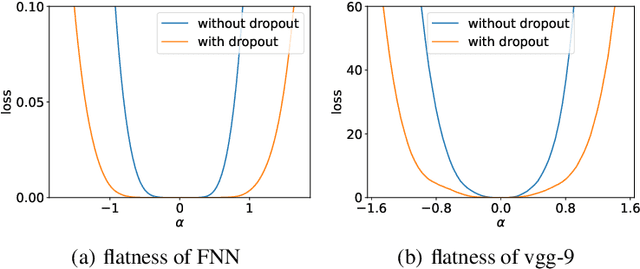
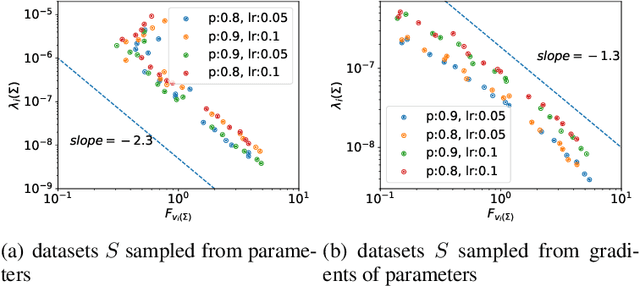
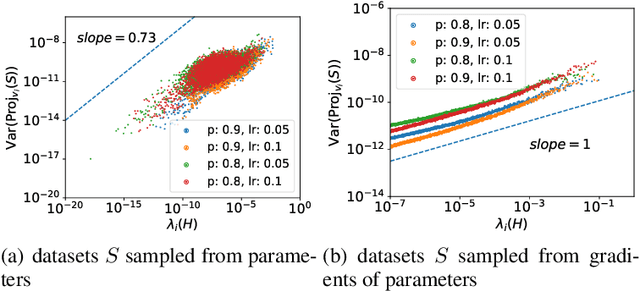
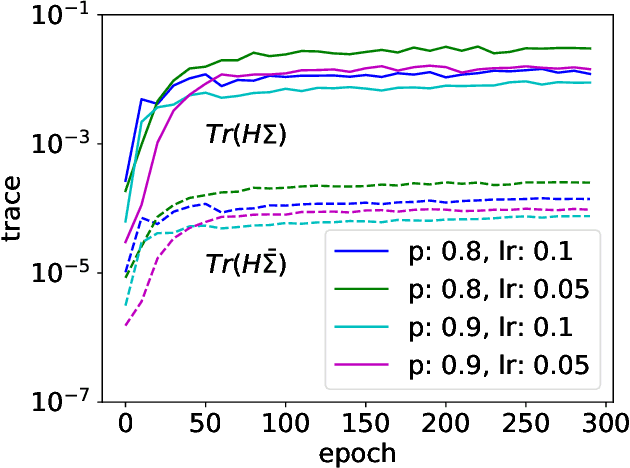
Although dropout has achieved great success in deep learning, little is known about how it helps the training find a good generalization solution in the high-dimensional parameter space. In this work, we show that the training with dropout finds the neural network with a flatter minimum compared with standard gradient descent training. We further study the underlying mechanism of why dropout finds flatter minima through experiments. We propose a {\it Variance Principle} that the variance of a noise is larger at the sharper direction of the loss landscape. Existing works show that SGD satisfies the variance principle, which leads the training to flatter minima. Our work show that the noise induced by the dropout also satisfies the variance principle that explains why dropout finds flatter minima. In general, our work points out that the variance principle is an important similarity between dropout and SGD that lead the training to find flatter minima and obtain good generalization.