A Unified Algorithmic Framework for Multi-Dimensional Scaling
Paper and Code
Mar 30, 2010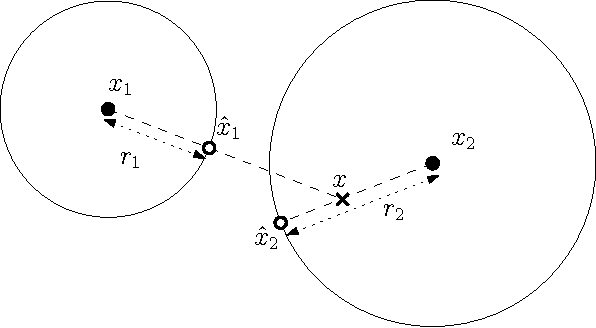

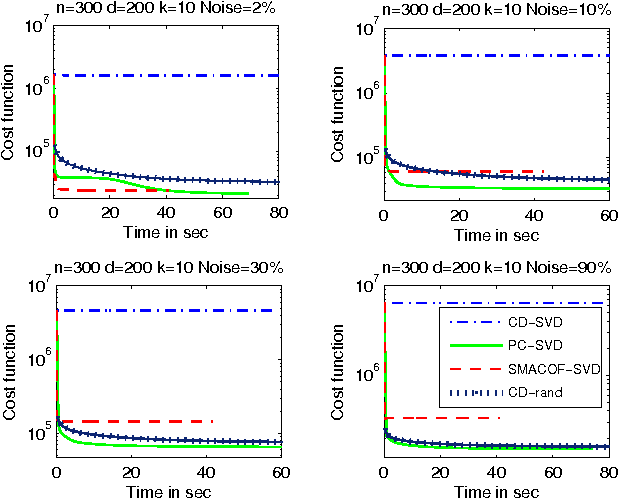
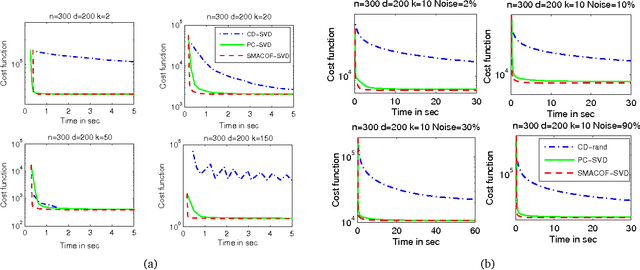
In this paper, we propose a unified algorithmic framework for solving many known variants of \mds. Our algorithm is a simple iterative scheme with guaranteed convergence, and is \emph{modular}; by changing the internals of a single subroutine in the algorithm, we can switch cost functions and target spaces easily. In addition to the formal guarantees of convergence, our algorithms are accurate; in most cases, they converge to better quality solutions than existing methods, in comparable time. We expect that this framework will be useful for a number of \mds variants that have not yet been studied. Our framework extends to embedding high-dimensional points lying on a sphere to points on a lower dimensional sphere, preserving geodesic distances. As a compliment to this result, we also extend the Johnson-Lindenstrauss Lemma to this spherical setting, where projecting to a random $O((1/\eps^2) \log n)$-dimensional sphere causes $\eps$-distortion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge