A Theoretical Analysis of Nash Learning from Human Feedback under General KL-Regularized Preference

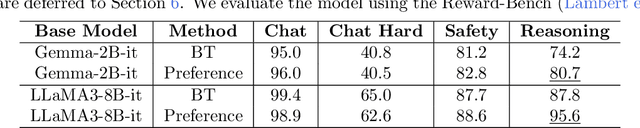
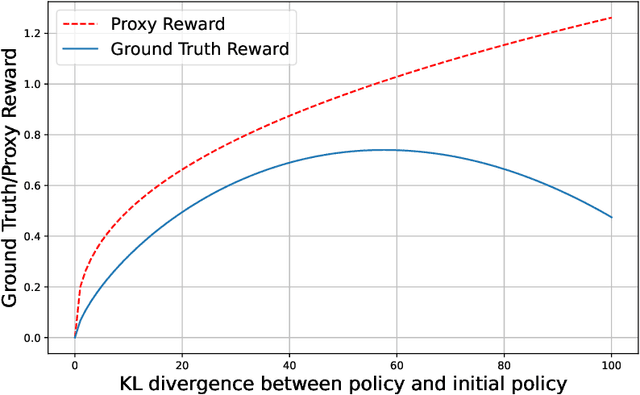
Reinforcement Learning from Human Feedback (RLHF) learns from the preference signal provided by a probabilistic preference model, which takes a prompt and two responses as input, and produces a score indicating the preference of one response against another. So far, the most popular RLHF paradigm is reward-based, which starts with an initial step of reward modeling, and the constructed reward is then used to provide a reward signal for the subsequent reward optimization stage. However, the existence of a reward function is a strong assumption and the reward-based RLHF is limited in expressivity and cannot capture the real-world complicated human preference. In this work, we provide theoretical insights for a recently proposed learning paradigm, Nash learning from human feedback (NLHF), which considered a general preference model and formulated the alignment process as a game between two competitive LLMs. The learning objective is to find a policy that consistently generates responses preferred over any competing policy while staying close to the initial model. The objective is defined as the Nash equilibrium (NE) of the KL-regularized preference model. We aim to make the first attempt to study the theoretical learnability of the KL-regularized NLHF by considering both offline and online settings. For the offline learning from a pre-collected dataset, we propose algorithms that are efficient under suitable coverage conditions of the dataset. For batch online learning from iterative interactions with a preference oracle, our proposed algorithm enjoys a finite sample guarantee under the structural condition of the underlying preference model. Our results connect the new NLHF paradigm with traditional RL theory, and validate the potential of reward-model-free learning under general preference.