A Survey of Recent Scalability Improvements for Semidefinite Programming with Applications in Machine Learning, Control, and Robotics
Paper and Code
Aug 14, 2019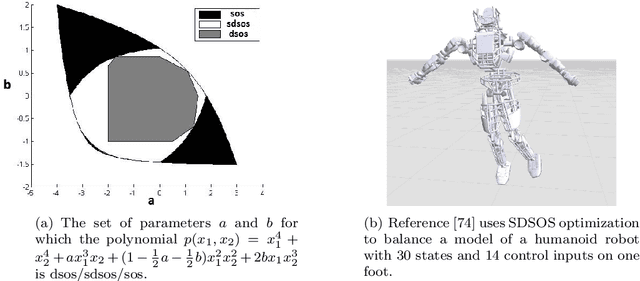
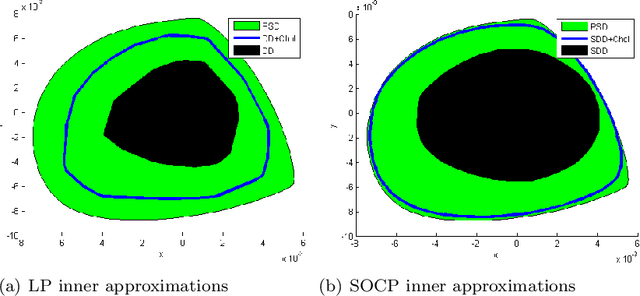
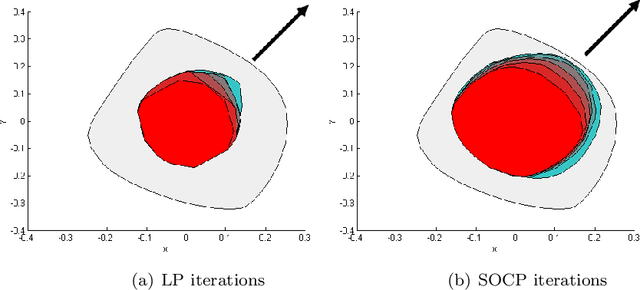
Historically, scalability has been a major challenge to the successful application of semidefinite programming in fields such as machine learning, control, and robotics. In this paper, we survey recent approaches for addressing this challenge including (i) approaches for exploiting structure (e.g., sparsity and symmetry) in a problem, (ii) approaches that produce low-rank approximate solutions to semidefinite programs, (iii) more scalable algorithms that rely on augmented Lagrangian techniques and the alternating direction method of multipliers, and (iv) approaches that trade off scalability with conservatism (e.g., by approximating semidefinite programs with linear and second-order cone programs). For each class of approaches we provide a high-level exposition, an entry-point to the corresponding literature, and examples drawn from machine learning, control, or robotics. We also present a list of software packages that implement many of the techniques discussed in the paper. Our hope is that this paper will serve as a gateway to the rich and exciting literature on scalable semidefinite programming for both theorists and practitioners.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge