A statistical interpretation of spectral embedding: the generalised random dot product graph

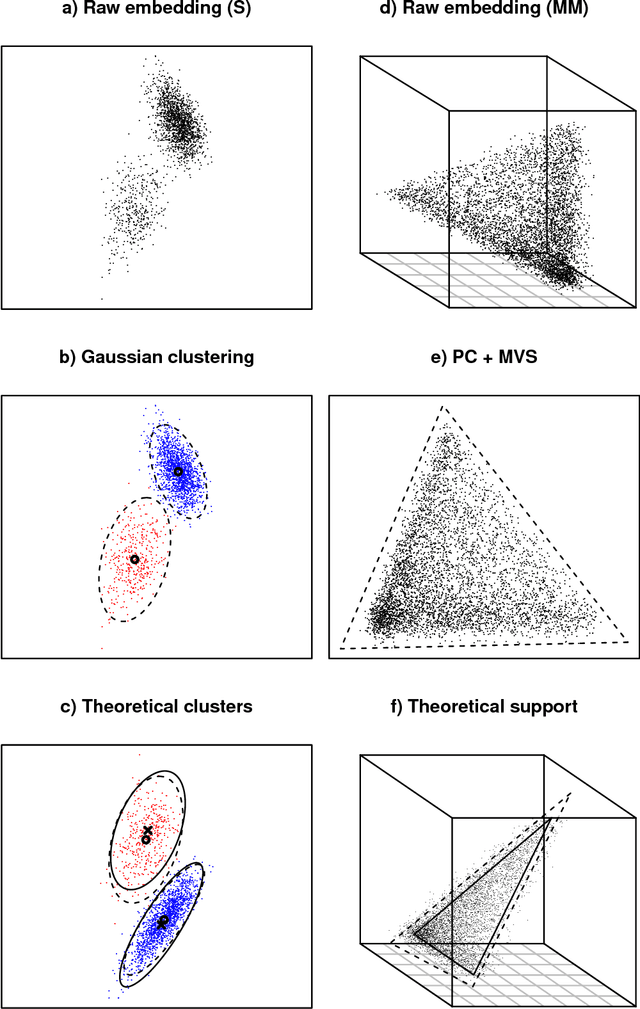
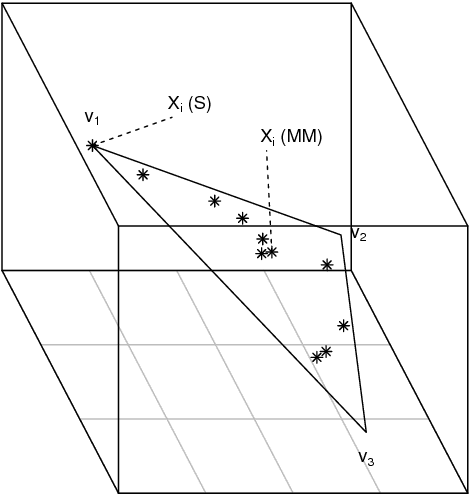
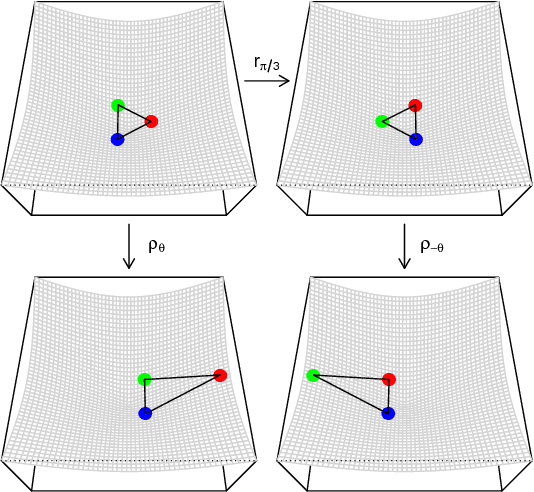
A generalisation of a latent position network model known as the random dot product graph model is considered. The resulting model may be of independent interest because it has the unique property of representing a mixture of connectivity behaviours as the corresponding convex combination in latent space. We show that, whether the normalised Laplacian or adjacency matrix is used, the vector representations of nodes obtained by spectral embedding provide strongly consistent latent position estimates with asymptotically Gaussian error. Direct methodological consequences follow from the observation that the well-known mixed membership and standard stochastic block models are special cases where the latent positions live respectively inside or on the vertices of a simplex. Estimation via spectral embedding can therefore be achieved by respectively estimating this simplicial support, or fitting a Gaussian mixture model. In the latter case, the use of $K$-means, as has been previously recommended, is suboptimal and for identifiability reasons unsound. Empirical improvements in link prediction, as well as the potential to uncover much richer latent structure (than available under the mixed membership or standard stochastic block models) are demonstrated in a cyber-security example.