A Sharp Analysis of Model-based Reinforcement Learning with Self-Play
Paper and Code
Oct 04, 2020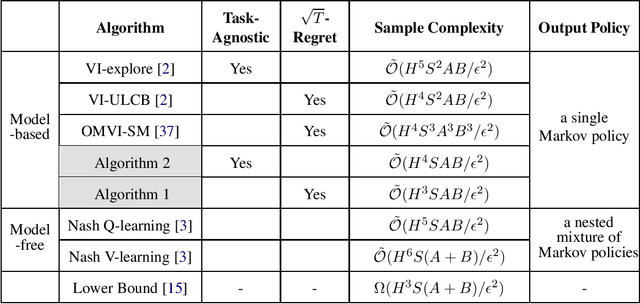
Model-based algorithms---algorithms that decouple learning of the model and planning given the model---are widely used in reinforcement learning practice and theoretically shown to achieve optimal sample efficiency for single-agent reinforcement learning in Markov Decision Processes (MDPs). However, for multi-agent reinforcement learning in Markov games, the current best known sample complexity for model-based algorithms is rather suboptimal and compares unfavorably against recent model-free approaches. In this paper, we present a sharp analysis of model-based self-play algorithms for multi-agent Markov games. We design an algorithm \emph{Optimistic Nash Value Iteration} (Nash-VI) for two-player zero-sum Markov games that is able to output an $\epsilon$-approximate Nash policy in $\tilde{\mathcal{O}}(H^3SAB/\epsilon^2)$ episodes of game playing, where $S$ is the number of states, $A,B$ are the number of actions for the two players respectively, and $H$ is the horizon length. This is the first algorithm that matches the information-theoretic lower bound $\Omega(H^3S(A+B)/\epsilon^2)$ except for a $\min\{A,B\}$ factor, and compares favorably against the best known model-free algorithm if $\min\{A,B\}=o(H^3)$. In addition, our Nash-VI outputs a single Markov policy with optimality guarantee, while existing sample-efficient model-free algorithms output a nested mixture of Markov policies that is in general non-Markov and rather inconvenient to store and execute. We further adapt our analysis to designing a provably efficient task-agnostic algorithm for zero-sum Markov games, and designing the first line of provably sample-efficient algorithms for multi-player general-sum Markov games.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge