A Ranking Game for Imitation Learning
Paper and Code
Feb 07, 2022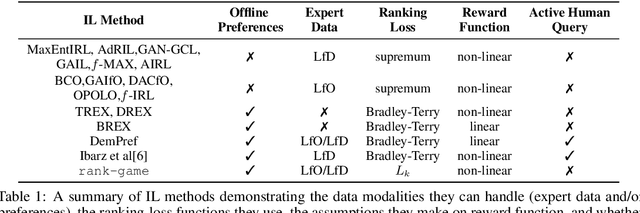
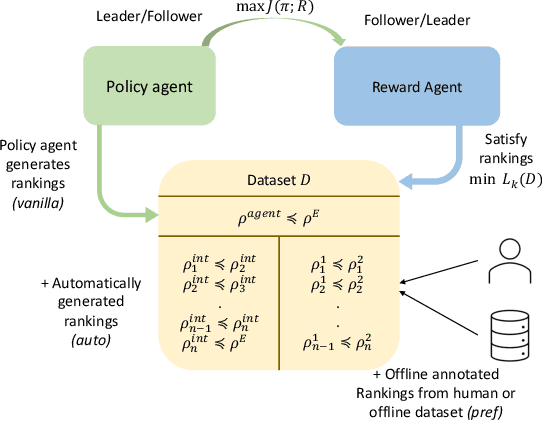
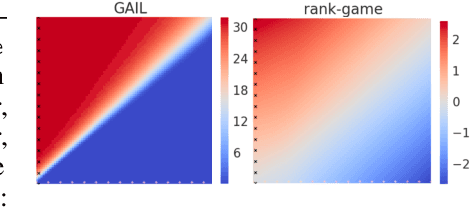
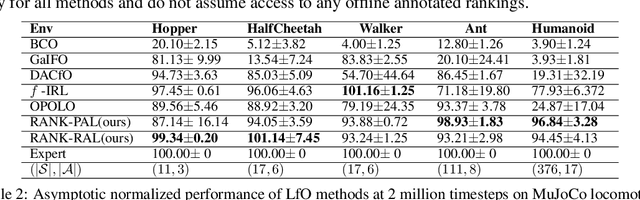
We propose a new framework for imitation learning - treating imitation as a two-player ranking-based Stackelberg game between a $\textit{policy}$ and a $\textit{reward}$ function. In this game, the reward agent learns to satisfy pairwise performance rankings within a set of policies, while the policy agent learns to maximize this reward. This game encompasses a large subset of both inverse reinforcement learning (IRL) methods and methods which learn from offline preferences. The Stackelberg game formulation allows us to use optimization methods that take the game structure into account, leading to more sample efficient and stable learning dynamics compared to existing IRL methods. We theoretically analyze the requirements of the loss function used for ranking policy performances to facilitate near-optimal imitation learning at equilibrium. We use insights from this analysis to further increase sample efficiency of the ranking game by using automatically generated rankings or with offline annotated rankings. Our experiments show that the proposed method achieves state-of-the-art sample efficiency and is able to solve previously unsolvable tasks in the Learning from Observation (LfO) setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge