A Provably Efficient Sample Collection Strategy for Reinforcement Learning

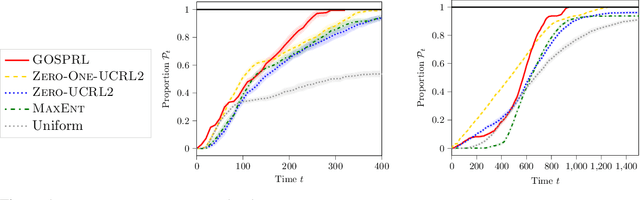
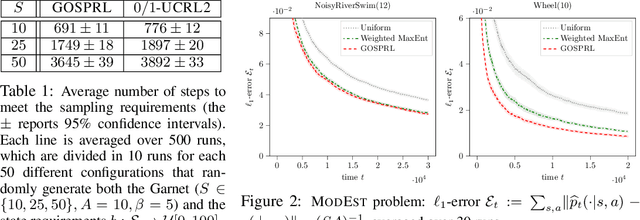
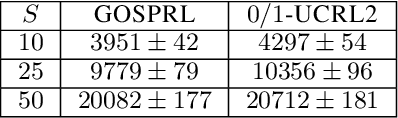
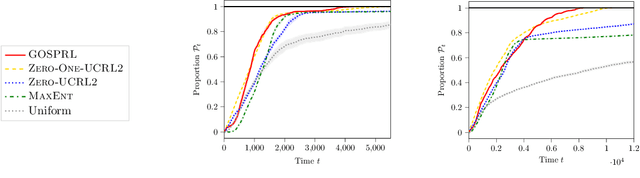
A common assumption in reinforcement learning (RL) is to have access to a generative model (i.e., a simulator of the environment), which allows to generate samples from any desired state-action pair. Nonetheless, in many settings a generative model may not be available and an adaptive exploration strategy is needed to efficiently collect samples from an unknown environment by direct interaction. In this paper, we study the scenario where an algorithm based on the generative model assumption defines the (possibly time-varying) amount of samples $b(s,a)$ required at each state-action pair $(s,a)$ and an exploration strategy has to learn how to generate $b(s,a)$ samples as fast as possible. Building on recent results for regret minimization in the stochastic shortest path (SSP) setting (Cohen et al., 2020; Tarbouriech et al., 2020), we derive an algorithm that requires $\tilde{O}( B D + D^{3/2} S^2 A)$ time steps to collect the $B = \sum_{s,a} b(s,a)$ desired samples, in any unknown and communicating MDP with $S$ states, $A$ actions and diameter $D$. Leveraging the generality of our strategy, we readily apply it to a variety of existing settings (e.g., model estimation, pure exploration in MDPs) for which we obtain improved sample-complexity guarantees, and to a set of new problems such as best-state identification and sparse reward discovery.