A PAC RL Algorithm for Episodic POMDPs
Paper and Code
Jun 01, 2016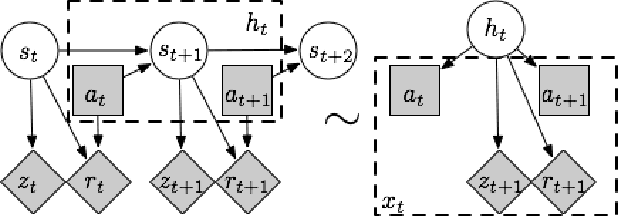
Many interesting real world domains involve reinforcement learning (RL) in partially observable environments. Efficient learning in such domains is important, but existing sample complexity bounds for partially observable RL are at least exponential in the episode length. We give, to our knowledge, the first partially observable RL algorithm with a polynomial bound on the number of episodes on which the algorithm may not achieve near-optimal performance. Our algorithm is suitable for an important class of episodic POMDPs. Our approach builds on recent advances in method of moments for latent variable model estimation.
* Proceedings of the 19th International Conference on Artificial
Intelligence and Statistics, pp. 510-518, 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge