A Novel Gradient Descent Least Squares (GDLS) Algorithm for SMV Gridless Line Spectrum Estimation with Efficiency

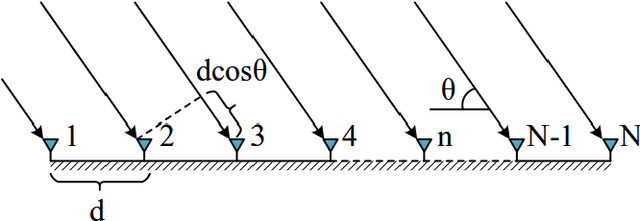
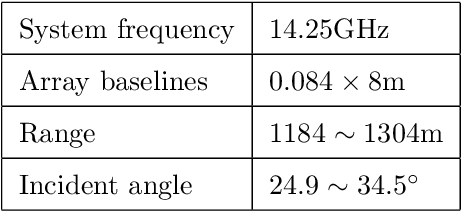
This paper presents a novel efficient method for gridless line spectrum estimation problem with single snapshot, namely the gradient descent least squares (GDLS) method. Conventional single snapshot (a.k.a. SMV measurement) line spectrum estimation methods either rely on smoothing techniques that sacrifice the array aperture, or adopt the sparsity constraint and utilize compressed sensing (CS) method by defining prior grids and resulting in the off-grid problem. Recently emerged atomic norm minimization (ANM) methods achieved gridless SMV line spectrum estimation, but its computational complexity is extremely high; thus it is practically infeasible in real applications with large problem scales. Our proposed GDLS method reformulates the line spectrum estimations problem into a least squares (LS) estimation problem and solves the corresponding objective function via gradient descent algorithm in an iterative fashion with efficiency. The convergence guarantee, computational complexity, as well as performance analysis are discussed in this paper. Numerical simulations and real data experiments show that the proposed GDLS algorithm outperforms the state-of-the-art methods e.g., CS and ANM, in terms of estimation performances. It can completely avoid the off-grid problem, and its computational complexity is significantly lower than ANM. Our method shows great potential in various applications e.g. direction of arrival (DOA) estimation and tomographic synthetic aperture radar (TomoSAR) imaging.