A Nonparametric Off-Policy Policy Gradient
Paper and Code
Feb 11, 2020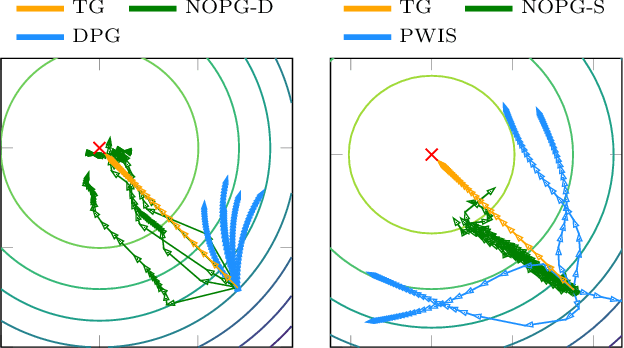



Reinforcement learning (RL) algorithms still suffer from high sample complexity despite outstanding recent successes. The need for intensive interactions with the environment is especially observed in many widely popular policy gradient algorithms that perform updates using on-policy samples. The price of such inefficiency becomes evident in real-world scenarios such as interaction-driven robot learning, where the success of RL has been rather limited. We address this issue by building on the general sample efficiency of off-policy algorithms. With nonparametric regression and density estimation methods we construct a nonparametric Bellman equation in a principled manner, which allows us to obtain closed-form estimates of the value function, and to analytically express the full policy gradient. We provide a theoretical analysis of our estimate to show that it is consistent under mild smoothness assumptions and empirically show that our approach has better sample efficiency than state-of-the-art policy gradient methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge