A new neighborhood structure for job shop scheduling problems
Paper and Code
Sep 07, 2021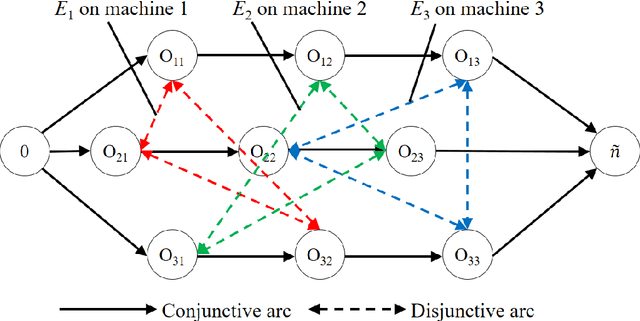
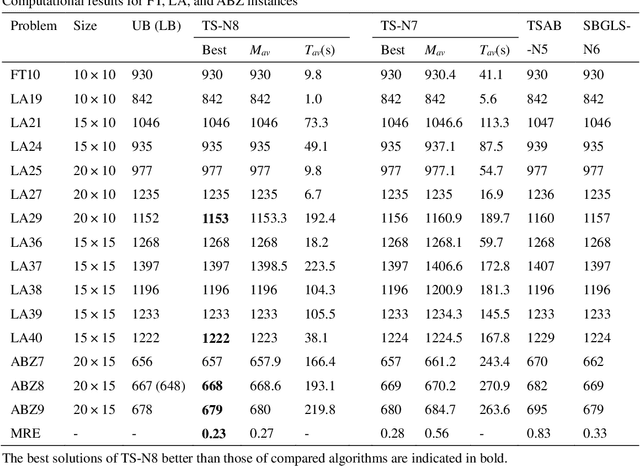
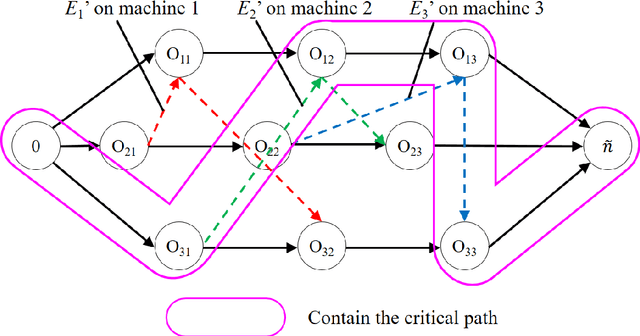
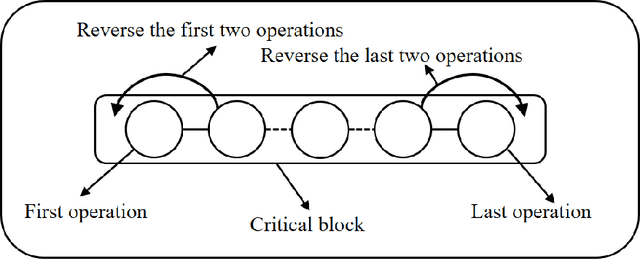
Job shop scheduling problem (JSP) is a widely studied NP-complete combinatorial optimization problem. Neighborhood structures play a critical role in solving JSP. At present, there are three state-of-the-art neighborhood structures, i.e., N5, N6, and N7. Improving the upper bounds of some famous benchmarks is inseparable from the role of these neighborhood structures. However, these existing neighborhood structures only consider the movement of critical operations within a critical block. According to our experiments, it is also possible to improve the makespan of a scheduling scheme by moving a critical operation outside its critical block. According to the above finding, this paper proposes a new N8 neighborhood structure considering the movement of critical operations within a critical block and the movement of critical operations outside the critical block. Besides, a neighborhood clipping method is designed to avoid invalid movement, reducing the computational time. Tabu search (TS) is a commonly used algorithm framework combined with neighborhood structures. This paper uses this framework to compare the N8 neighborhood structure with N5, N6, and N7 neighborhood structures on four famous benchmarks. The experimental results verify that the N8 neighborhood structure is more effective and efficient in solving JSP than the other state-of-the-art neighborhood structures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge