A New Many-Objective Evolutionary Algorithm Based on Determinantal Point Processes
Paper and Code
Dec 15, 2020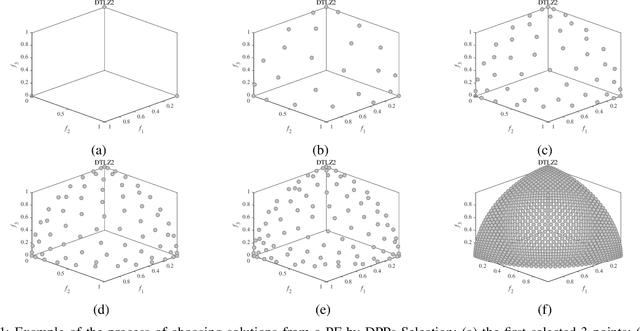
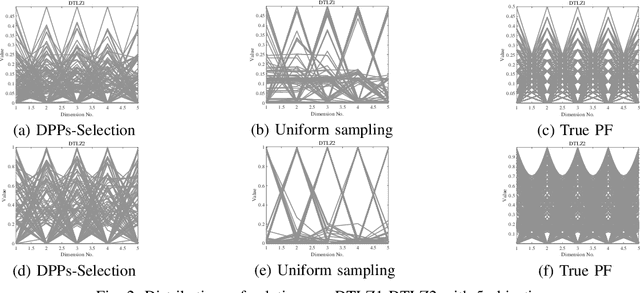
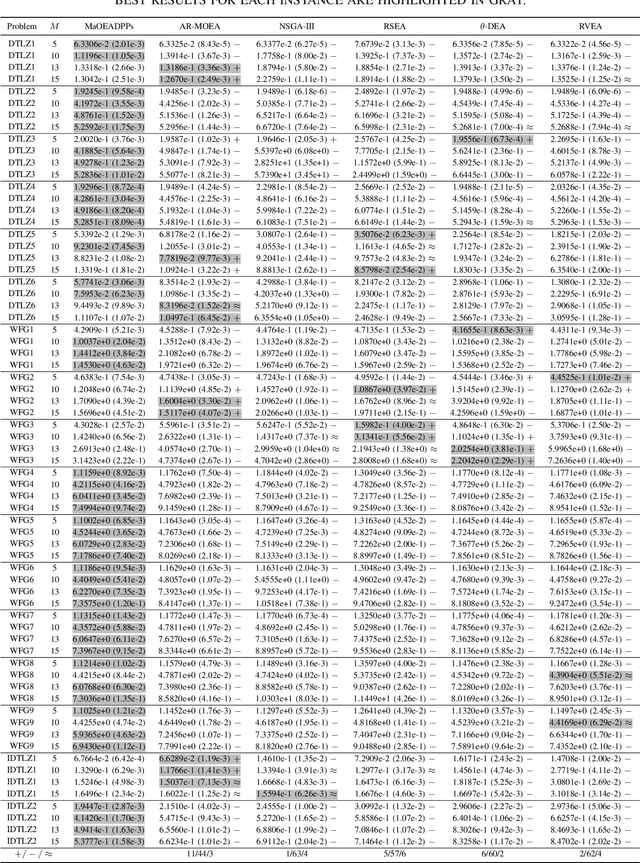
To handle different types of Many-Objective Optimization Problems (MaOPs), Many-Objective Evolutionary Algorithms (MaOEAs) need to simultaneously maintain convergence and population diversity in the high-dimensional objective space. In order to balance the relationship between diversity and convergence, we introduce a Kernel Matrix and probability model called Determinantal Point Processes (DPPs). Our Many-Objective Evolutionary Algorithm with Determinantal Point Processes (MaOEADPPs) is presented and compared with several state-of-the-art algorithms on various types of MaOPs \textcolor{blue}{with different numbers of objectives}. The experimental results demonstrate that MaOEADPPs is competitive.
* 12 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge