A model of sensory neural responses in the presence of unknown modulatory inputs
Paper and Code
Jul 07, 2015
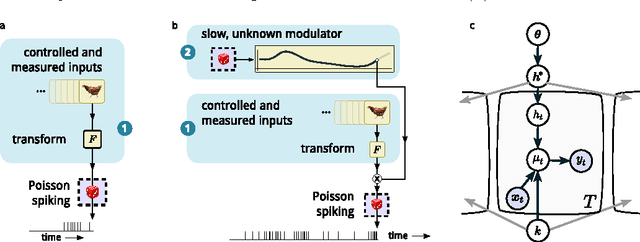
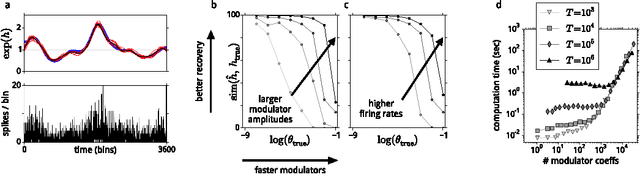
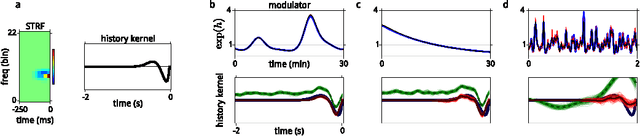
Neural responses are highly variable, and some portion of this variability arises from fluctuations in modulatory factors that alter their gain, such as adaptation, attention, arousal, expected or actual reward, emotion, and local metabolic resource availability. Regardless of their origin, fluctuations in these signals can confound or bias the inferences that one derives from spiking responses. Recent work demonstrates that for sensory neurons, these effects can be captured by a modulated Poisson model, whose rate is the product of a stimulus-driven response function and an unknown modulatory signal. Here, we extend this model, by incorporating explicit modulatory elements that are known (specifically, spike-history dependence, as in previous models), and by constraining the remaining latent modulatory signals to be smooth in time. We develop inference procedures for fitting the entire model, including hyperparameters, via evidence optimization, and apply these to simulated data, and to responses of ferret auditory midbrain and cortical neurons to complex sounds. We show that integrating out the latent modulators yields better (or more readily-interpretable) receptive field estimates than a standard Poisson model. Conversely, integrating out the stimulus dependence yields estimates of the slowly-varying latent modulators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge