A Minimum-Jerk Approach to Handle Singularities in Virtual Fixtures
Paper and Code
May 06, 2024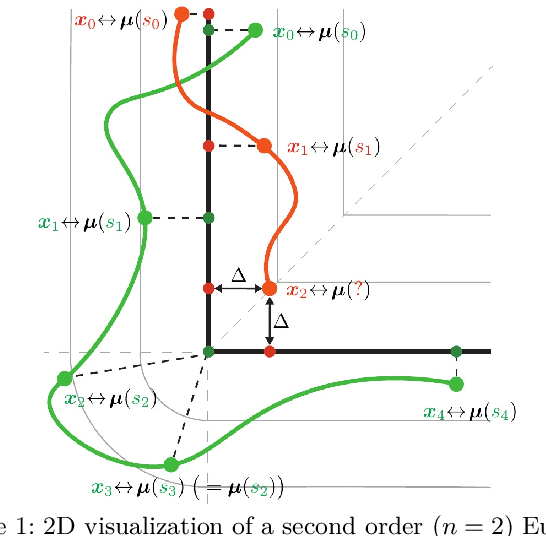

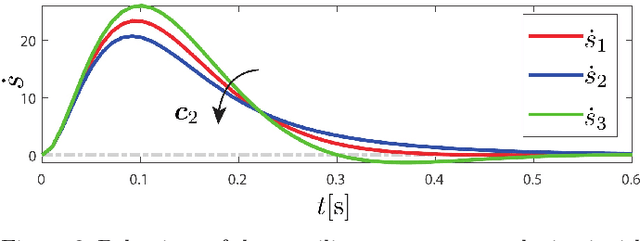

Implementing virtual fixtures in guiding tasks constrains the movement of the robot's end effector to specific curves within its workspace. However, incorporating guiding frameworks may encounter discontinuities when optimizing the reference target position to the nearest point relative to the current robot position. This article aims to give a geometric interpretation of such discontinuities, with specific reference to the commonly adopted Gauss-Newton algorithm. The effect of such discontinuities, defined as Euclidean Distance Singularities, is experimentally proved. We then propose a solution that is based on a Linear Quadratic Tracking problem with minimum jerk command, then compare and validate the performances of the proposed framework in two different human-robot interaction scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge