A Mean Field Theory of Batch Normalization
Paper and Code
Mar 05, 2019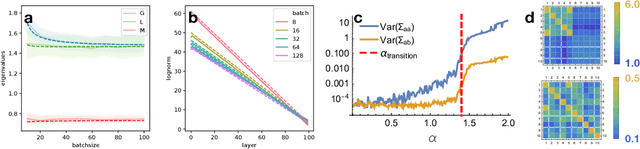
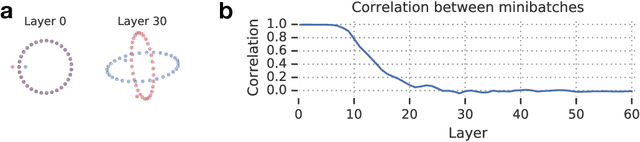
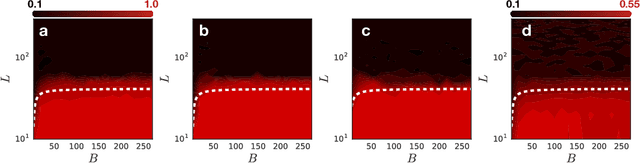
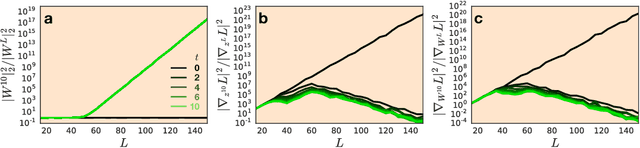
We develop a mean field theory for batch normalization in fully-connected feedforward neural networks. In so doing, we provide a precise characterization of signal propagation and gradient backpropagation in wide batch-normalized networks at initialization. Our theory shows that gradient signals grow exponentially in depth and that these exploding gradients cannot be eliminated by tuning the initial weight variances or by adjusting the nonlinear activation function. Indeed, batch normalization itself is the cause of gradient explosion. As a result, vanilla batch-normalized networks without skip connections are not trainable at large depths for common initialization schemes, a prediction that we verify with a variety of empirical simulations. While gradient explosion cannot be eliminated, it can be reduced by tuning the network close to the linear regime, which improves the trainability of deep batch-normalized networks without residual connections. Finally, we investigate the learning dynamics of batch-normalized networks and observe that after a single step of optimization the networks achieve a relatively stable equilibrium in which gradients have dramatically smaller dynamic range. Our theory leverages Laplace, Fourier, and Gegenbauer transforms and we derive new identities that may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge