A Hybrid Stochastic Optimization Framework for Stochastic Composite Nonconvex Optimization
Paper and Code
Jul 08, 2019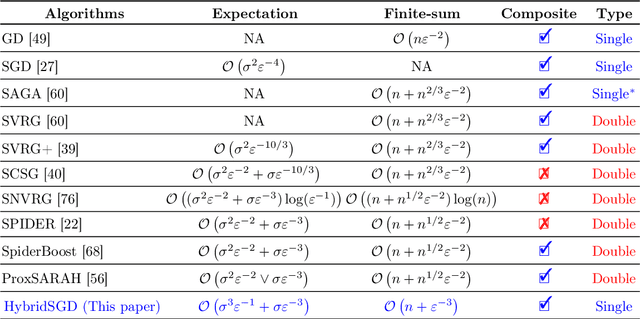
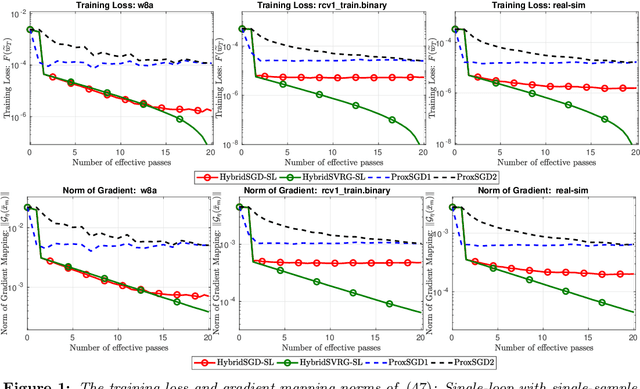
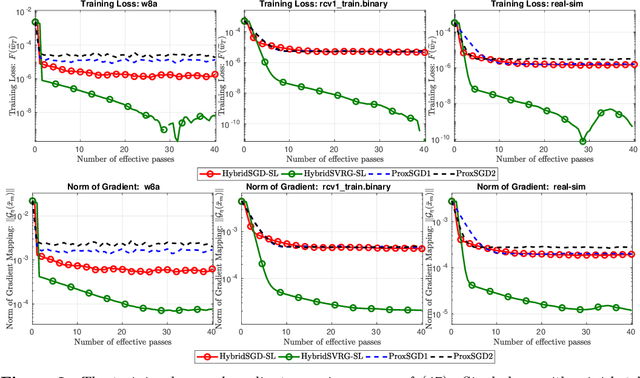
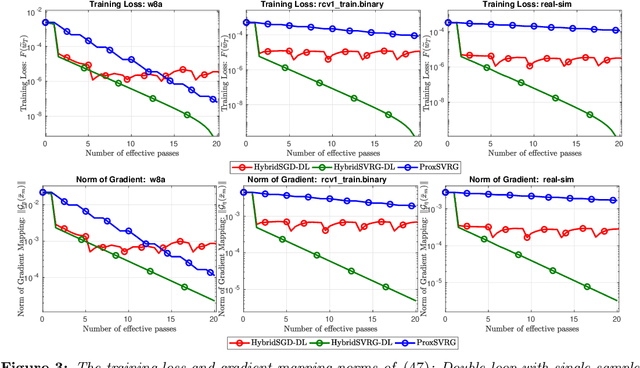
In this paper, we introduce a new approach to develop stochastic optimization algorithms for solving stochastic composite and possibly nonconvex optimization problems. The main idea is to combine two stochastic estimators to form a new hybrid one. We first introduce our hybrid estimator and then investigate its fundamental properties to form a foundation theory for algorithmic development. Next, we apply our theory to develop several variants of stochastic gradient methods to solve both expectation and finite-sum composite optimization problems. Our first algorithm can be viewed as a variant of proximal stochastic gradient methods with a single-loop, but can achieve $\mathcal{O}(\sigma^3\varepsilon^{-1} + \sigma\varepsilon^{-3})$ complexity bound that is significantly better than the $\mathcal{O}(\sigma^2\varepsilon^{-4})$-complexity in state-of-the-art stochastic gradient methods, where $\sigma$ is the variance and $\varepsilon$ is a desired accuracy. Then, we consider two different variants of our method: adaptive step-size and double-loop schemes that have the same theoretical guarantees as in our first algorithm. We also study two mini-batch variants and develop two hybrid SARAH-SVRG algorithms to solve the finite-sum problems. In all cases, we achieve the best-known complexity bounds under standard assumptions. We test our methods on several numerical examples with real datasets and compare them with state-of-the-arts. Our numerical experiments show that the new methods are comparable and, in many cases, outperform their competitors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge