A Generalized Algorithm for Multi-Objective Reinforcement Learning and Policy Adaptation

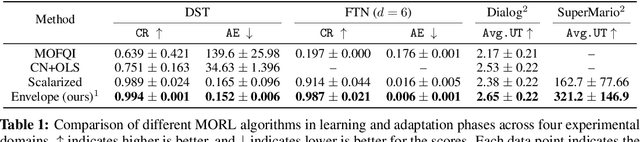
We introduce a new algorithm for multi-objective reinforcement learning (MORL) with linear preferences, with the goal of enabling few-shot adaptation to new tasks. In MORL, the aim is to learn policies over multiple competing objectives whose relative importance (preferences) is unknown to the agent. While this alleviates dependence on scalar reward design, the expected return of a policy can change significantly with varying preferences, making it challenging to learn a single model to produce optimal policies under different preference conditions. We propose a generalized version of the Bellman equation to learn a single parametric representation for optimal policies over the space of all possible preferences. After this initial learning phase, our agent can quickly adapt to any given preference, or automatically infer an underlying preference with very few samples. Experiments across four different domains demonstrate the effectiveness of our approach.