A General Deep Learning Speech Enhancement Framework Motivated by Taylor's Theorem
Paper and Code
Nov 30, 2022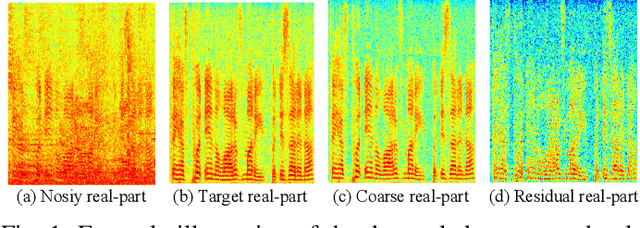
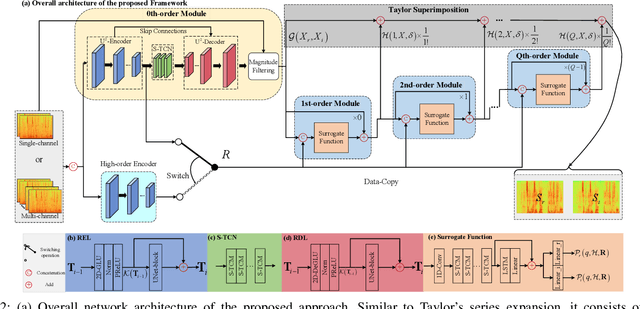
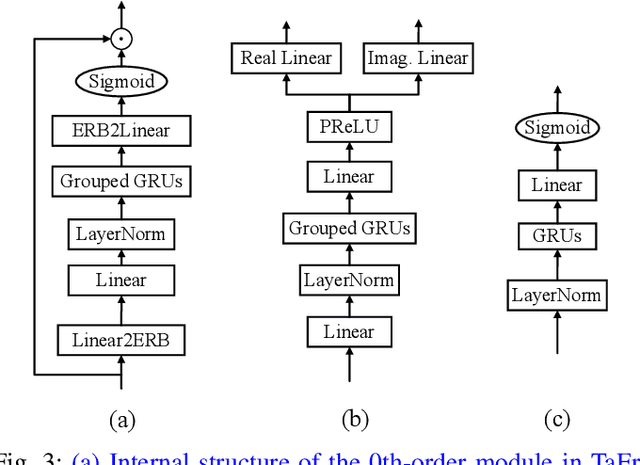
While deep neural networks greatly facilitate the proliferation of the speech enhancement field, most of the existing methods are developed following either heuristic or blind optimization criteria, which severely hampers interpretability and transparency. Inspired by Taylor's theorem, we propose a general unfolding framework for both single- and multi-channel speech enhancement tasks. Concretely, we formulate the complex spectrum recovery into the spectral magnitude mapping in the neighboring space of the noisy mixture, in which the sparse prior is introduced for phase modification in advance. Based on that, the mapping function is decomposed into the superimposition of the 0th-order and high-order polynomials in Taylor's series, where the former coarsely removes the interference in the magnitude domain and the latter progressively complements the remaining spectral detail in the complex spectrum domain. In addition, we study the relation between adjacent order term and reveal that each high-order term can be recursively estimated with its lower-order term, and each high-order term is then proposed to evaluate using a surrogate function with trainable weights, so that the whole system can be trained in an end-to-end manner. Extensive experiments are conducted on WSJ0-SI84, DNS-Challenge, Voicebank+Demand, and spatialized Librispeech datasets. Quantitative results show that the proposed approach not only yields competitive performance over existing top-performed approaches, but also enjoys decent internal transparency and flexibility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge