A Frequency-Domain Encoding for Neuroevolution
Paper and Code
Dec 28, 2012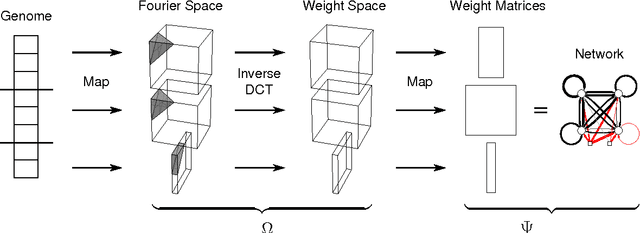
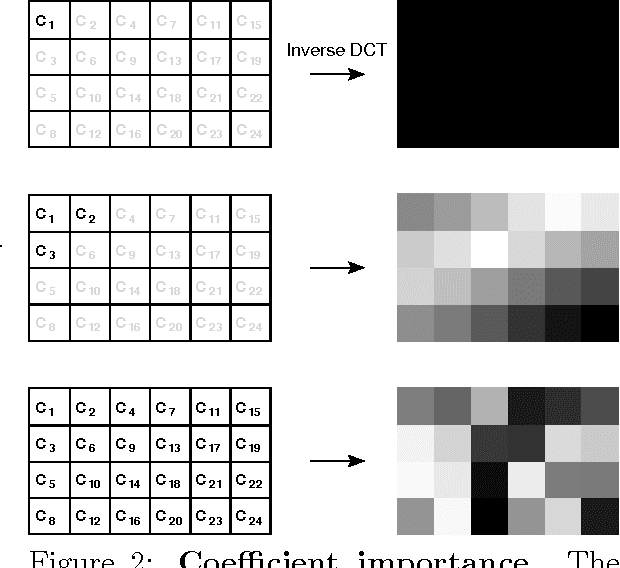
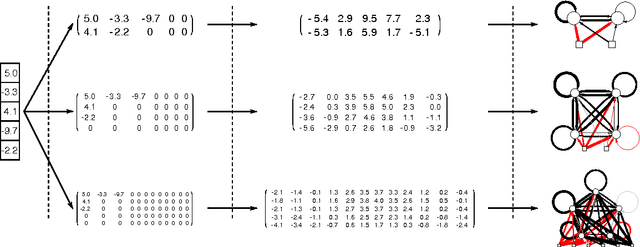
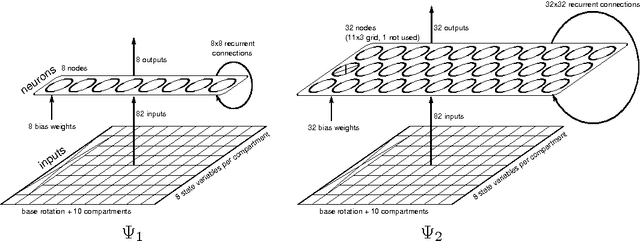
Neuroevolution has yet to scale up to complex reinforcement learning tasks that require large networks. Networks with many inputs (e.g. raw video) imply a very high dimensional search space if encoded directly. Indirect methods use a more compact genotype representation that is transformed into networks of potentially arbitrary size. In this paper, we present an indirect method where networks are encoded by a set of Fourier coefficients which are transformed into network weight matrices via an inverse Fourier-type transform. Because there often exist network solutions whose weight matrices contain regularity (i.e. adjacent weights are correlated), the number of coefficients required to represent these networks in the frequency domain is much smaller than the number of weights (in the same way that natural images can be compressed by ignore high-frequency components). This "compressed" encoding is compared to the direct approach where search is conducted in the weight space on the high-dimensional octopus arm task. The results show that representing networks in the frequency domain can reduce the search-space dimensionality by as much as two orders of magnitude, both accelerating convergence and yielding more general solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge