A First-Order Algorithm for Graph Learning from Smooth Signals Under Partial Observability
Paper and Code
Oct 08, 2024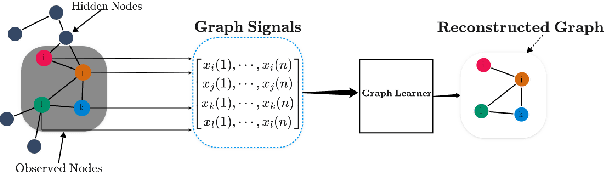

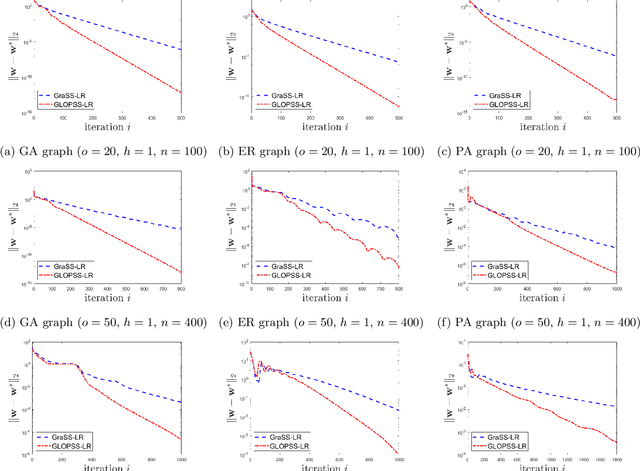
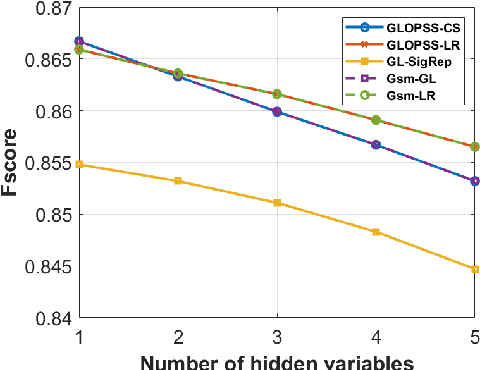
Learning graph structures from smooth signals is a significant problem in data science and engineering. A common challenge in real-world scenarios is the availability of only partially observed nodes. While some studies have considered hidden nodes and proposed various optimization frameworks, existing methods often lack the practical efficiency needed for large-scale networks or fail to provide theoretical convergence guarantees. In this paper, we address the problem of inferring network topologies from smooth signals with partially observed nodes. We propose a first-order algorithmic framework that includes two variants: one based on column sparsity regularization and the other on a low-rank constraint. We establish theoretical convergence guarantees and demonstrate the linear convergence rate of our algorithms. Extensive experiments on both synthetic and real-world data show that our results align with theoretical predictions, exhibiting not only linear convergence but also superior speed compared to existing methods. To the best of our knowledge, this is the first work to propose a first-order algorithmic framework for inferring network structures from smooth signals under partial observability, offering both guaranteed linear convergence and practical effectiveness for large-scale networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge