A-expansion for multiple "hedgehog" shapes
Paper and Code
Feb 02, 2016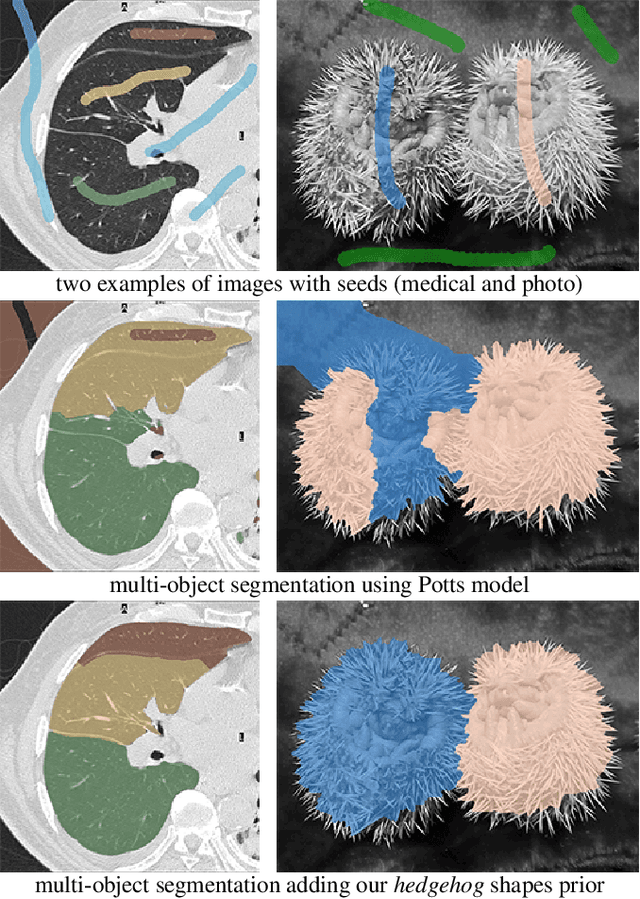
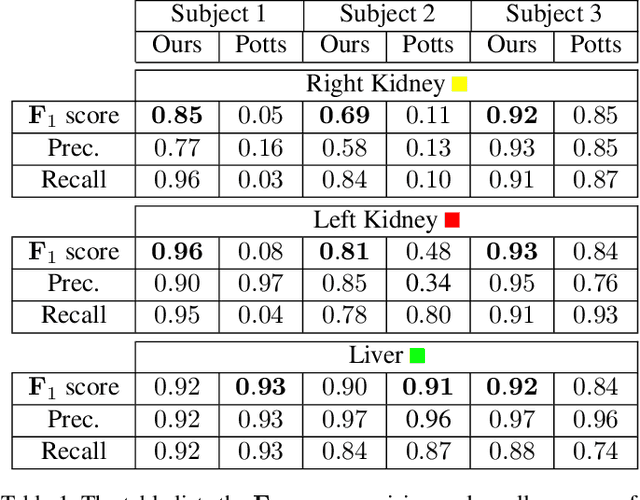
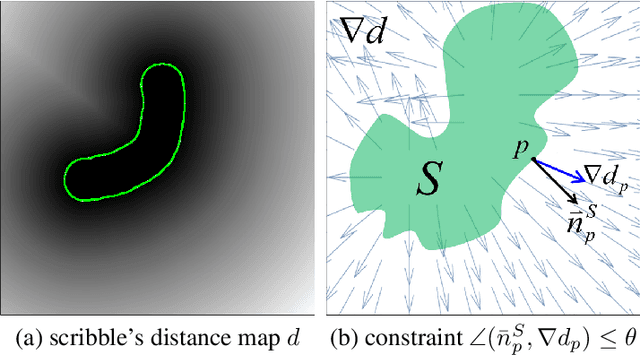
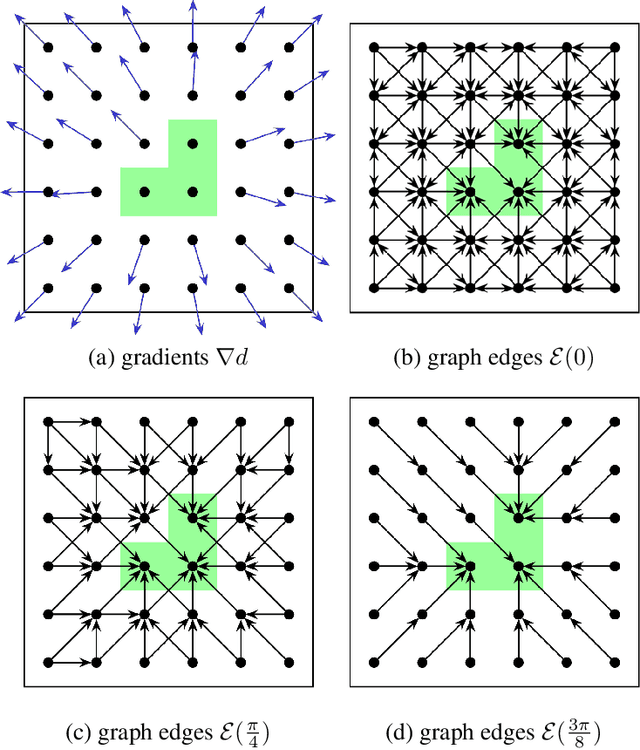
Overlapping colors and cluttered or weak edges are common segmentation problems requiring additional regularization. For example, star-convexity is popular for interactive single object segmentation due to simplicity and amenability to exact graph cut optimization. This paper proposes an approach to multiobject segmentation where objects could be restricted to separate "hedgehog" shapes. We show that a-expansion moves are submodular for our multi-shape constraints. Each "hedgehog" shape has its surface normals constrained by some vector field, e.g. gradients of a distance transform for user scribbles. Tight constraint give an extreme case of a shape prior enforcing skeleton consistency with the scribbles. Wider cones of allowed normals gives more relaxed hedgehog shapes. A single click and +/-90 degrees normal orientation constraints reduce our hedgehog prior to star-convexity. If all hedgehogs come from single clicks then our approach defines multi-star prior. Our general method has significantly more applications than standard one-star segmentation. For example, in medical data we can separate multiple non-star organs with similar appearances and weak or noisy edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge