A Deterministic Analysis of an Online Convex Mixture of Expert Algorithms

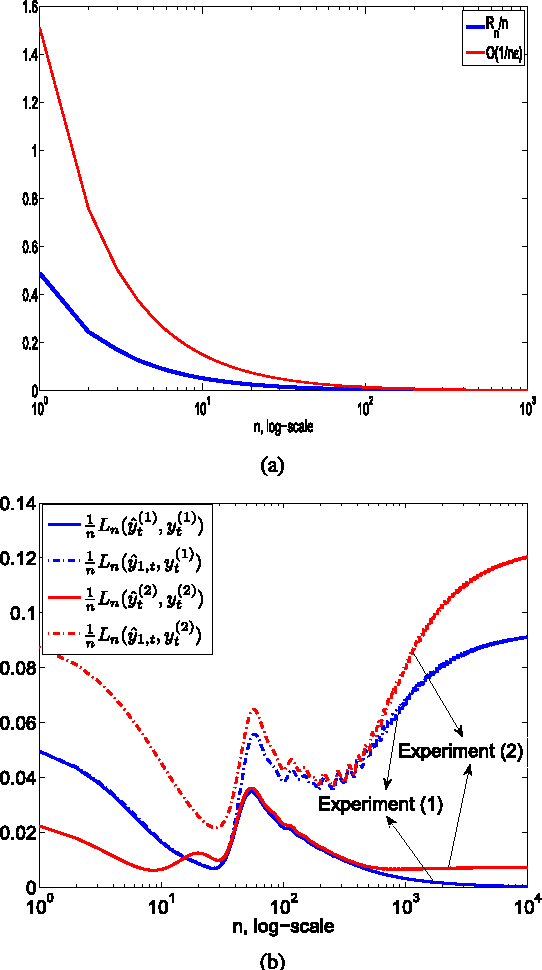
We analyze an online learning algorithm that adaptively combines outputs of two constituent algorithms (or the experts) running in parallel to model an unknown desired signal. This online learning algorithm is shown to achieve (and in some cases outperform) the mean-square error (MSE) performance of the best constituent algorithm in the mixture in the steady-state. However, the MSE analysis of this algorithm in the literature uses approximations and relies on statistical models on the underlying signals and systems. Hence, such an analysis may not be useful or valid for signals generated by various real life systems that show high degrees of nonstationarity, limit cycles and, in many cases, that are even chaotic. In this paper, we produce results in an individual sequence manner. In particular, we relate the time-accumulated squared estimation error of this online algorithm at any time over any interval to the time accumulated squared estimation error of the optimal convex mixture of the constituent algorithms directly tuned to the underlying signal in a deterministic sense without any statistical assumptions. In this sense, our analysis provides the transient, steady-state and tracking behavior of this algorithm in a strong sense without any approximations in the derivations or statistical assumptions on the underlying signals such that our results are guaranteed to hold. We illustrate the introduced results through examples.