A Complexity-Based Theory of Compositionality
Paper and Code
Oct 18, 2024
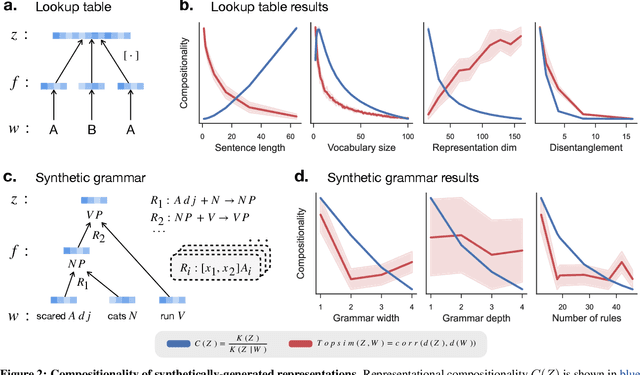
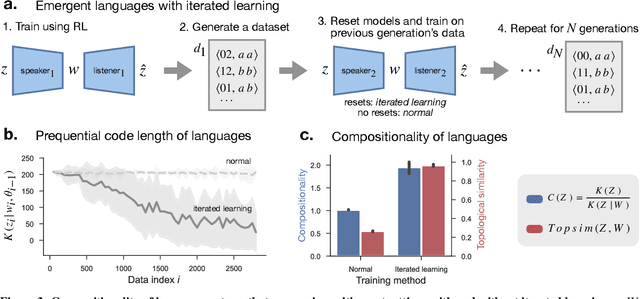
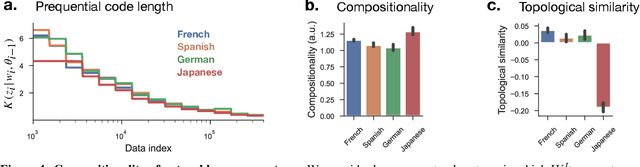
Compositionality is believed to be fundamental to intelligence. In humans, it underlies the structure of thought, language, and higher-level reasoning. In AI, compositional representations can enable a powerful form of out-of-distribution generalization, in which a model systematically adapts to novel combinations of known concepts. However, while we have strong intuitions about what compositionality is, there currently exists no formal definition for it that is measurable and mathematical. Here, we propose such a definition, which we call representational compositionality, that accounts for and extends our intuitions about compositionality. The definition is conceptually simple, quantitative, grounded in algorithmic information theory, and applicable to any representation. Intuitively, representational compositionality states that a compositional representation satisfies three properties. First, it must be expressive. Second, it must be possible to re-describe the representation as a function of discrete symbolic sequences with re-combinable parts, analogous to sentences in natural language. Third, the function that relates these symbolic sequences to the representation, analogous to semantics in natural language, must be simple. Through experiments on both synthetic and real world data, we validate our definition of compositionality and show how it unifies disparate intuitions from across the literature in both AI and cognitive science. We also show that representational compositionality, while theoretically intractable, can be readily estimated using standard deep learning tools. Our definition has the potential to inspire the design of novel, theoretically-driven models that better capture the mechanisms of compositional thought.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge