A Closer Look at Robustness to L-infinity and Spatial Perturbations and their Composition
Paper and Code
Oct 05, 2022
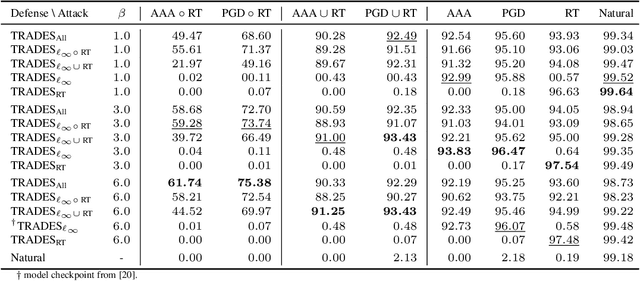
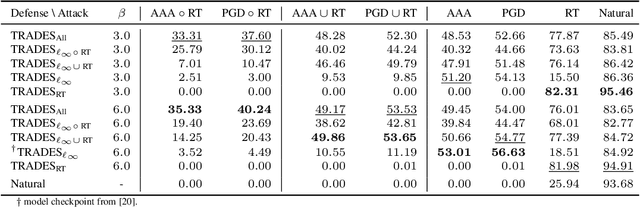
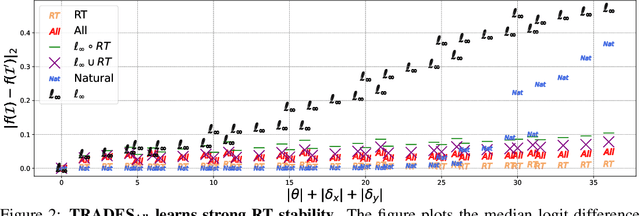
In adversarial machine learning, the popular $\ell_\infty$ threat model has been the focus of much previous work. While this mathematical definition of imperceptibility successfully captures an infinite set of additive image transformations that a model should be robust to, this is only a subset of all transformations which leave the semantic label of an image unchanged. Indeed, previous work also considered robustness to spatial attacks as well as other semantic transformations; however, designing defense methods against the composition of spatial and $\ell_{\infty}$ perturbations remains relatively underexplored. In the following, we improve the understanding of this seldom investigated compositional setting. We prove theoretically that no linear classifier can achieve more than trivial accuracy against a composite adversary in a simple statistical setting, illustrating its difficulty. We then investigate how state-of-the-art $\ell_{\infty}$ defenses can be adapted to this novel threat model and study their performance against compositional attacks. We find that our newly proposed TRADES$_{\text{All}}$ strategy performs the strongest of all. Analyzing its logit's Lipschitz constant for RT transformations of different sizes, we find that TRADES$_{\text{All}}$ remains stable over a wide range of RT transformations with and without $\ell_\infty$ perturbations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge