Gradient Descent Methods for Regularized Optimization

Regularization is a widely recognized technique in mathematical optimization. It can be used to smooth out objective functions, refine the feasible solution set, or prevent overfitting in machine learning models. Due to its simplicity and robustness, the gradient descent (GD) method is one of the primary methods used for numerical optimization of differentiable objective functions. However, GD is not well-suited for solving $\ell^1$ regularized optimization problems since these problems are non-differentiable at zero, causing iteration updates to oscillate or fail to converge. Instead, a more effective version of GD, called the proximal gradient descent employs a technique known as soft-thresholding to shrink the iteration updates toward zero, thus enabling sparsity in the solution. Motivated by the widespread applications of proximal GD in sparse and low-rank recovery across various engineering disciplines, we provide an overview of the GD and proximal GD methods for solving regularized optimization problems. Furthermore, this paper proposes a novel algorithm for the proximal GD method that incorporates a variable step size. Unlike conventional proximal GD, which uses a fixed step size based on the global Lipschitz constant, our method estimates the Lipschitz constant locally at each iteration and uses its reciprocal as the step size. This eliminates the need for a global Lipschitz constant, which can be impractical to compute. Numerical experiments we performed on synthetic and real-data sets show notable performance improvement of the proposed method compared to the conventional proximal GD with constant step size, both in terms of number of iterations and in time requirements.

Convergence Rate Maximization for Split Learning-based Control of EMG Prosthetic Devices

Split Learning (SL) is a promising Distributed Learning approach in electromyography (EMG) based prosthetic control, due to its applicability within resource-constrained environments. Other learning approaches, such as Deep Learning and Federated Learning (FL), provide suboptimal solutions, since prosthetic devices are extremely limited in terms of processing power and battery life. The viability of implementing SL in such scenarios is caused by its inherent model partitioning, with clients executing the smaller model segment. However, selecting an inadequate cut layer hinders the training process in SL systems. This paper presents an algorithm for optimal cut layer selection in terms of maximizing the convergence rate of the model. The performance evaluation demonstrates that the proposed algorithm substantially accelerates the convergence in an EMG pattern recognition task for improving prosthetic device control.

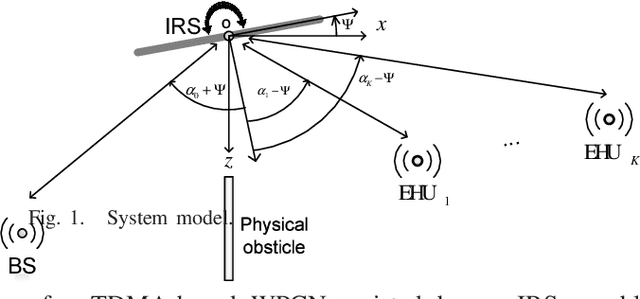
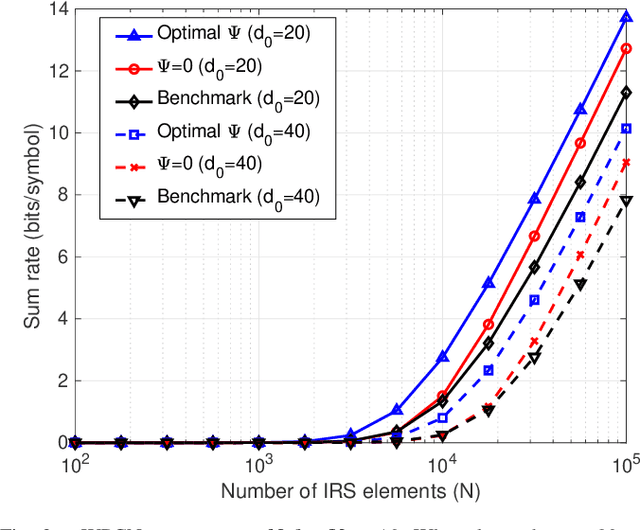
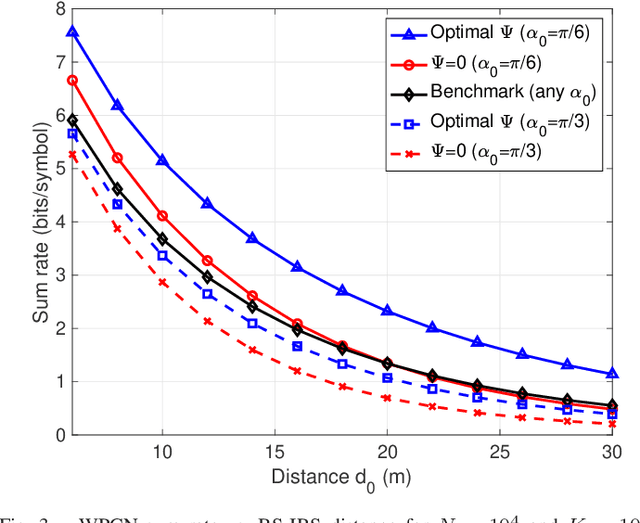
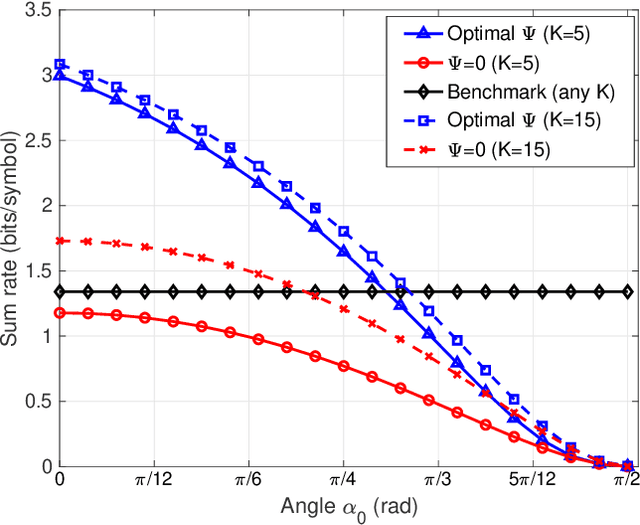
Designing Wireless Powered Networks assisted by Intelligent Reflecting Surfaces with Mechanical Tilt

In this paper, we propose a fairness-aware rate maximization scheme for a wireless powered communications network (WPCN) assisted by an intelligent reflecting surface (IRS). The proposed scheme combines user scheduling based on time division multiple access (TDMA) and (mechanical) angular displacement of the IRS. Each energy harvesting user (EHU) has dedicated time slots with optimized durations for energy harvesting and information transmission whereas, the phase matrix of the IRS is adjusted to focus its beam to a particular EHU. The proposed scheme exploits the fundamental dependence of the IRS channel path-loss on the angle between the IRS and the node's line-of-sight, which is often overlooked in the literature. Additionally, the network design can be optimized for large number of IRS unit cells, which is not the case with the computationally intensive state-of-the-art schemes. In fact, the EHUs can achieve significant rates at practical distances of several tens of meters to the base station (BS) only if the number of IRS unit cells is at least a few thousand.