ExOSITO: Explainable Off-Policy Learning with Side Information for Intensive Care Unit Blood Test Orders

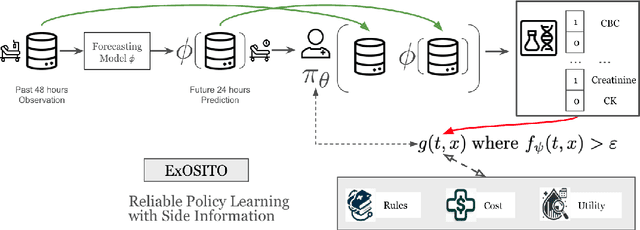
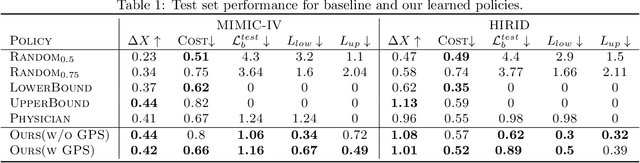
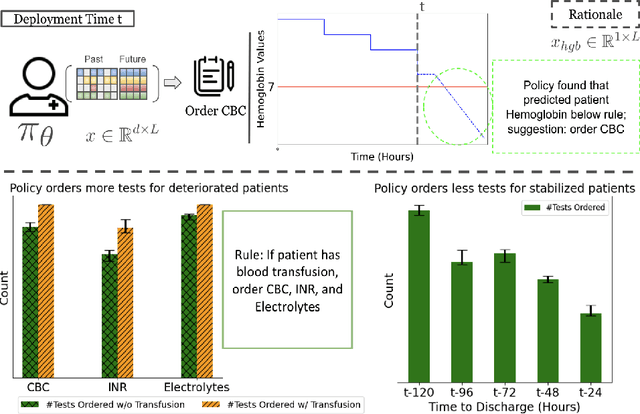
Ordering a minimal subset of lab tests for patients in the intensive care unit (ICU) can be challenging. Care teams must balance between ensuring the availability of the right information and reducing the clinical burden and costs associated with each lab test order. Most in-patient settings experience frequent over-ordering of lab tests, but are now aiming to reduce this burden on both hospital resources and the environment. This paper develops a novel method that combines off-policy learning with privileged information to identify the optimal set of ICU lab tests to order. Our approach, EXplainable Off-policy learning with Side Information for ICU blood Test Orders (ExOSITO) creates an interpretable assistive tool for clinicians to order lab tests by considering both the observed and predicted future status of each patient. We pose this problem as a causal bandit trained using offline data and a reward function derived from clinically-approved rules; we introduce a novel learning framework that integrates clinical knowledge with observational data to bridge the gap between the optimal and logging policies. The learned policy function provides interpretable clinical information and reduces costs without omitting any vital lab orders, outperforming both a physician's policy and prior approaches to this practical problem.

Measurement Scheduling for ICU Patients with Offline Reinforcement Learning

Scheduling laboratory tests for ICU patients presents a significant challenge. Studies show that 20-40% of lab tests ordered in the ICU are redundant and could be eliminated without compromising patient safety. Prior work has leveraged offline reinforcement learning (Offline-RL) to find optimal policies for ordering lab tests based on patient information. However, new ICU patient datasets have since been released, and various advancements have been made in Offline-RL methods. In this study, we first introduce a preprocessing pipeline for the newly-released MIMIC-IV dataset geared toward time-series tasks. We then explore the efficacy of state-of-the-art Offline-RL methods in identifying better policies for ICU patient lab test scheduling. Besides assessing methodological performance, we also discuss the overall suitability and practicality of using Offline-RL frameworks for scheduling laboratory tests in ICU settings.

Matrix Multiplication: Verifying Strong Uniquely Solvable Puzzles

Cohn and Umans proposed a framework for developing fast matrix multiplication algorithms based on the embedding computation in certain groups algebras. In subsequent work with Kleinberg and Szegedy, they connected this to the search for combinatorial objects called strong uniquely solvable puzzles (strong USPs). We begin a systematic computer-aided search for these objects. We develop and implement constraint-based algorithms build on reductions to $\mathrm{SAT}$ and $\mathrm{IP}$ to verify that puzzles are strong USPs, and to search for large strong USPs. We produce tight bounds on the maximum size of a strong USP for width $k \le 5$, construct puzzles of small width that are larger than previous work, and improve the upper bounds on strong USP size for $k \le 12$. Although our work only deals with puzzles of small-constant width, the strong USPs we find imply matrix multiplication algorithms that run in $O(n^\omega)$ time with exponent $\omega \le 2.66$. While our algorithms do not beat the fastest algorithms, our work provides evidence and, perhaps, a path to finding families of strong USPs that imply matrix multiplication algorithms that are more efficient than those currently known.