An Evaluation of Representation Learning Methods in Particle Physics Foundation Models

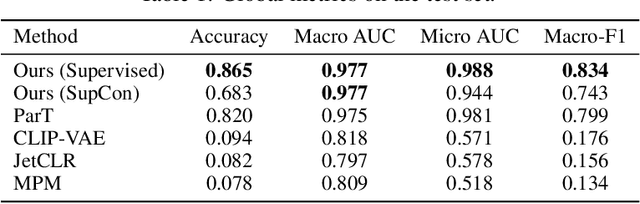
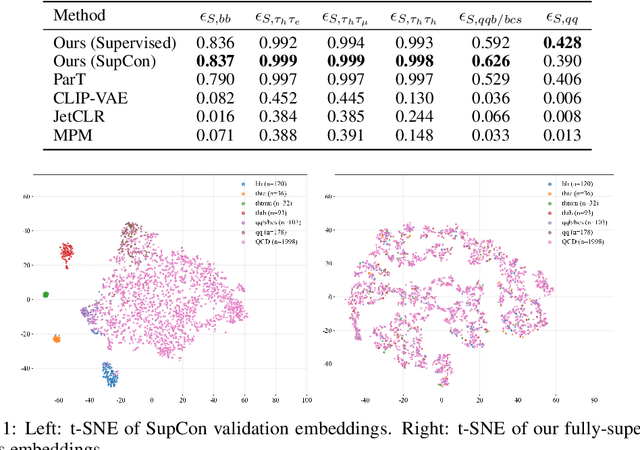
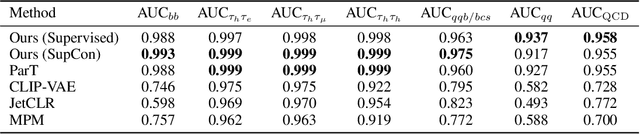
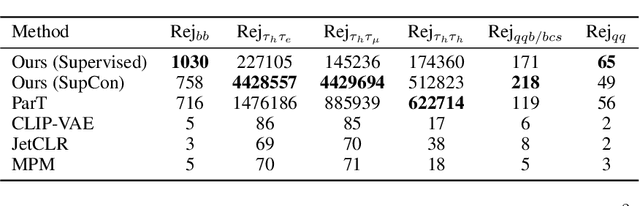
We present a systematic evaluation of representation learning objectives for particle physics within a unified framework. Our study employs a shared transformer-based particle-cloud encoder with standardized preprocessing, matched sampling, and a consistent evaluation protocol on a jet classification dataset. We compare contrastive (supervised and self-supervised), masked particle modeling, and generative reconstruction objectives under a common training regimen. In addition, we introduce targeted supervised architectural modifications that achieve state-of-the-art performance on benchmark evaluations. This controlled comparison isolates the contributions of the learning objective, highlights their respective strengths and limitations, and provides reproducible baselines. We position this work as a reference point for the future development of foundation models in particle physics, enabling more transparent and robust progress across the community.

RINO: Renormalization Group Invariance with No Labels

A common challenge with supervised machine learning (ML) in high energy physics (HEP) is the reliance on simulations for labeled data, which can often mismodel the underlying collision or detector response. To help mitigate this problem of domain shift, we propose RINO (Renormalization Group Invariance with No Labels), a self-supervised learning approach that can instead pretrain models directly on collision data, learning embeddings invariant to renormalization group flow scales. In this work, we pretrain a transformer-based model on jets originating from quantum chromodynamic (QCD) interactions from the JetClass dataset, emulating real QCD-dominated experimental data, and then finetune on the JetNet dataset -- emulating simulations -- for the task of identifying jets originating from top quark decays. RINO demonstrates improved generalization from the JetNet training data to JetClass data compared to supervised training on JetNet from scratch, demonstrating the potential for RINO pretraining on real collision data followed by fine-tuning on small, high-quality MC datasets, to improve the robustness of ML models in HEP.

Lorentz Group Equivariant Autoencoders

There has been significant work recently in developing machine learning models in high energy physics (HEP), for tasks such as classification, simulation, and anomaly detection. Typically, these models are adapted from those designed for datasets in computer vision or natural language processing without necessarily incorporating inductive biases suited to HEP data, such as respecting its inherent symmetries. Such inductive biases can make the model more performant and interpretable, and reduce the amount of training data needed. To that end, we develop the Lorentz group autoencoder (LGAE), an autoencoder model equivariant with respect to the proper, orthochronous Lorentz group $\mathrm{SO}^+(3,1)$, with a latent space living in the representations of the group. We present our architecture and several experimental results on jets at the LHC and find it significantly outperforms a non-Lorentz-equivariant graph neural network baseline on compression and reconstruction, and anomaly detection. We also demonstrate the advantage of such an equivariant model in analyzing the latent space of the autoencoder, which can have a significant impact on the explainability of anomalies found by such black-box machine learning models.