Multi-model Stochastic Particle-based Variational Bayesian Inference for Multiband Delay Estimation

Joint utilization of multiple discrete frequency bands can enhance the accuracy of delay estimation. Although some unique challenges of multiband fusion, such as phase distortion, oscillation phenomena, and high-dimensional search, have been partially addressed, further challenges remain. Specifically, under conditions of low signal-to-noise ratio (SNR), insufficient data, and closely spaced delay paths, accurately determining the model order-the number of delay paths-becomes difficult. Misestimating the model order can significantly degrade the estimation performance of traditional methods. To address joint model selection and parameter estimation under such harsh conditions, we propose a multi-model stochastic particle-based variational Bayesian inference (MM-SPVBI) framework, capable of exploring multiple high-dimensional parameter spaces. Initially, we split potential overlapping primary delay paths based on coarse estimates, generating several parallel candidate models. Then, an auto-focusing sampling strategy is employed to quickly identify the optimal model. Additionally, we introduce a hybrid posterior approximation to improve the original single-model SPVBI, ensuring overall complexity does not increase significantly with parallelism. Simulations demonstrate that our algorithm offers substantial advantages over existing methods.

A Stochastic Particle Variational Bayesian Inference Inspired Deep-Unfolding Network for Non-Convex Parameter Estimation

Future wireless networks are envisioned to provide ubiquitous sensing services, which also gives rise to a substantial demand for high-dimensional non-convex parameter estimation, i.e., the associated likelihood function is non-convex and contains numerous local optima. Variational Bayesian inference (VBI) provides a powerful tool for modeling complex estimation problems and reasoning with prior information, but poses a long-standing challenge on computing intractable posteriori distributions. Most existing variational methods generally rely on assumptions about specific distribution families to derive closed-form solutions, and are difficult to apply in high-dimensional, non-convex scenarios. Given these challenges, firstly, we propose a parallel stochastic particle variational Bayesian inference (PSPVBI) algorithm. Thanks to innovations such as particle approximation, additional updates of particle positions, and parallel stochastic successive convex approximation (PSSCA), PSPVBI can flexibly drive particles to fit the posteriori distribution with acceptable complexity, yielding high-precision estimates of the target parameters. Furthermore, additional speedup can be obtained by deep-unfolding (DU) the PSPVBI algorithm. Specifically, superior hyperparameters are learned to dramatically reduce the number of algorithmic iterations. In this PSPVBI-induced Deep-Unfolding Networks, some techniques related to gradient computation, data sub-sampling, differentiable sampling, and generalization ability are also employed to facilitate the practical deployment. Finally, we apply the LPSPVBI to solve several important parameter estimation problems in wireless sensing scenarios. Simulations indicate that the LPSPVBI algorithm outperforms existing solutions.

Stochastic Particle-Based Variational Bayesian Inference for Multi-band Radar Sensing

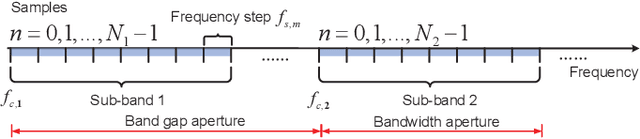
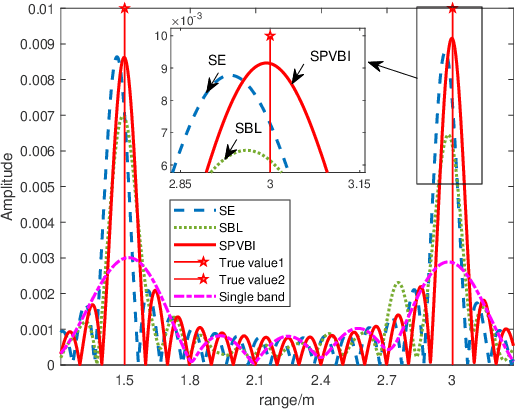
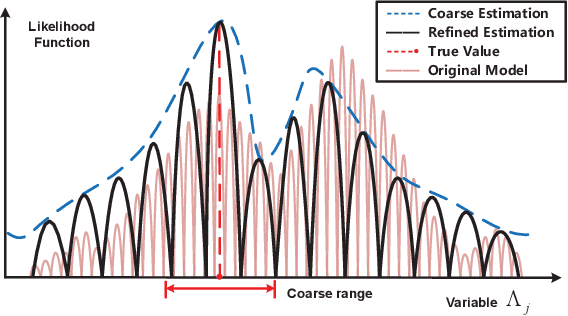
Multi-band fusion is an important technology to improve the radar sensing performance. In the multi-band radar sensing signal model, the associated likelihood function has oscillation phenomenon, which makes it difficult to obtain high-accuracy parameter estimation. To cope with this challenge, we divide the radar target parameter estimation into two stages of coarse estimation and refined estimation, where the coarse estimation is used to narrow down the search range for the refined estimation, and the refined estimation is based on the Bayesian approach to avoid the convergence to a bad local optimum of the likelihood function. Specifically, in the coarse estimation stage, we employ a root MUSIC algorithm to achieve initial estimation. Then, we apply the block stochastic successive convex approximation (SSCA) approach to derive a novel stochastic particle-based variational Bayesian inference (SPVBI) algorithm for the Bayesian estimation of the radar target parameters in the refined stage. Unlike the conventional particle-based VBI (PVBI) in which only the probability of each particle is optimized and the per-iteration computational complexity increases exponentially with the number of particles, the proposed SPVBI optimizes both the position and probability of each particle, and it adopts the block SSCA to significantly improve the sampling efficiency by averaging over iterations. As such, it is shown that the proposed SPVBI can achieve a better performance than the conventional PVBI with a much smaller number of particles and per-iteration complexity. Finally, extensive simulations verify the advantage of the proposed algorithm over various baseline algorithms.