When Does A Spectral Graph Neural Network Fail in Node Classification?

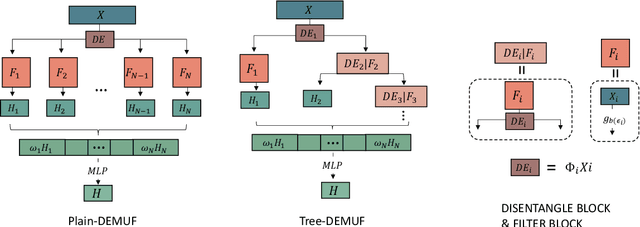
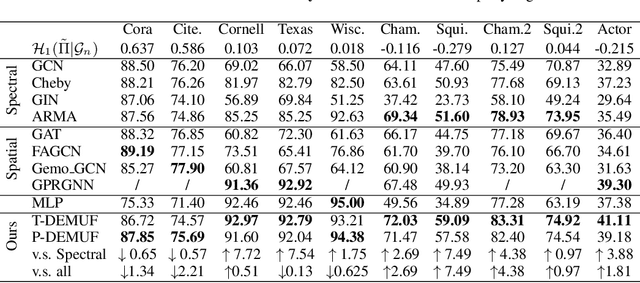
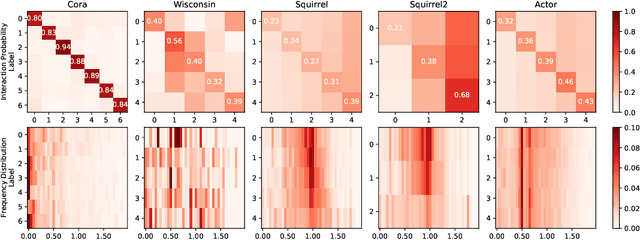
Spectral Graph Neural Networks (GNNs) with various graph filters have received extensive affirmation due to their promising performance in graph learning problems. However, it is known that GNNs do not always perform well. Although graph filters provide theoretical foundations for model explanations, it is unclear when a spectral GNN will fail. In this paper, focusing on node classification problems, we conduct a theoretical analysis of spectral GNNs performance by investigating their prediction error. With the aid of graph indicators including homophily degree and response efficiency we proposed, we establish a comprehensive understanding of complex relationships between graph structure, node labels, and graph filters. We indicate that graph filters with low response efficiency on label difference are prone to fail. To enhance GNNs performance, we provide a provably better strategy for filter design from our theoretical analysis - using data-driven filter banks, and propose simple models for empirical validation. Experimental results show consistency with our theoretical results and support our strategy.

Wasserstein diffusion on graphs with missing attributes

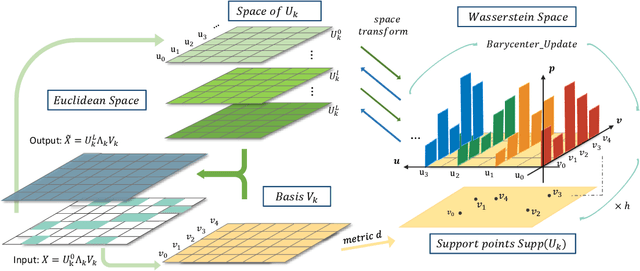
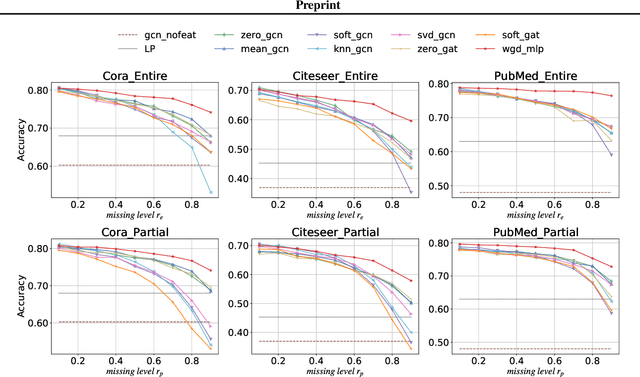
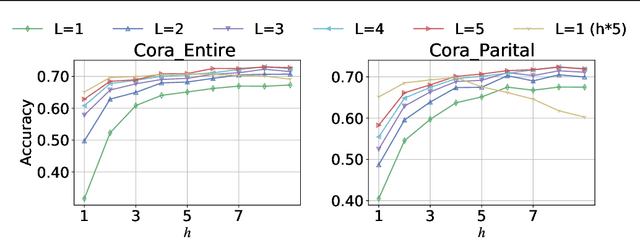
Missing node attributes is a common problem in real-world graphs. Graph neural networks have been demonstrated powerful in graph representation learning, however, they rely heavily on the completeness of graph information. Few of them consider the incomplete node attributes, which can bring great damage to the performance in practice. In this paper, we propose an innovative node representation learning framework, Wasserstein graph diffusion (WGD), to mitigate the problem. Instead of feature imputation, our method directly learns node representations from the missing-attribute graphs. Specifically, we extend the message passing schema in general graph neural networks to a Wasserstein space derived from the decomposition of attribute matrices. We test WGD in node classification tasks under two settings: missing whole attributes on some nodes and missing only partial attributes on all nodes. In addition, we find WGD is suitable to recover missing values and adapt it to tackle matrix completion problems with graphs of users and items. Experimental results on both tasks demonstrate the superiority of our method.

BiGCN: A Bi-directional Low-Pass Filtering Graph Neural Network

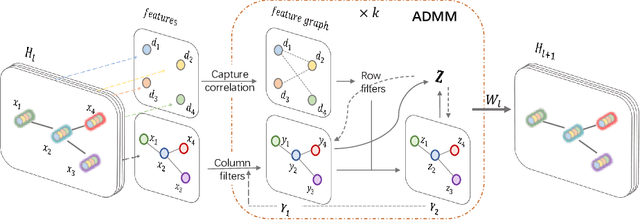
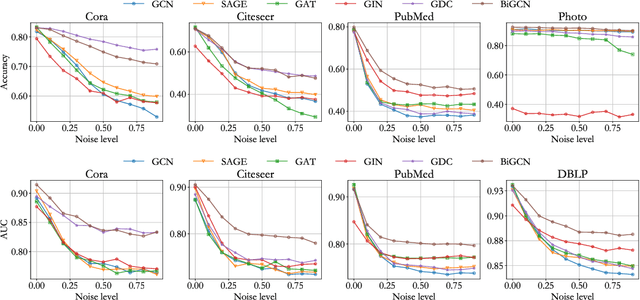
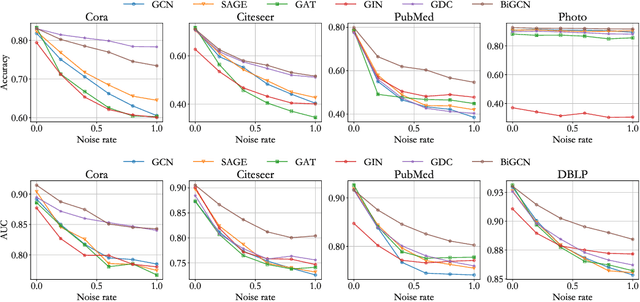
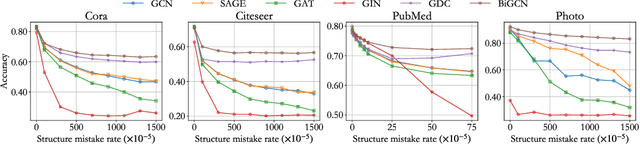
Graph convolutional networks have achieved great success on graph-structured data. Many graph convolutional networks can be regarded as low-pass filters for graph signals. In this paper, we propose a new model, BiGCN, which represents a graph neural network as a bi-directional low-pass filter. Specifically, we not only consider the original graph structure information but also the latent correlation between features, thus BiGCN can filter the signals along with both the original graph and a latent feature-connection graph. Our model outperforms previous graph neural networks in the tasks of node classification and link prediction on most of the benchmark datasets, especially when we add noise to the node features.