Split-and-Conquer: Distributed Factor Modeling for High-Dimensional Matrix-Variate Time Series

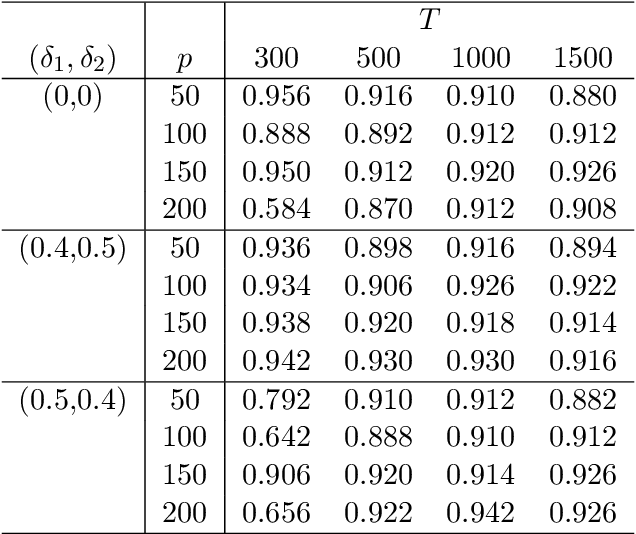
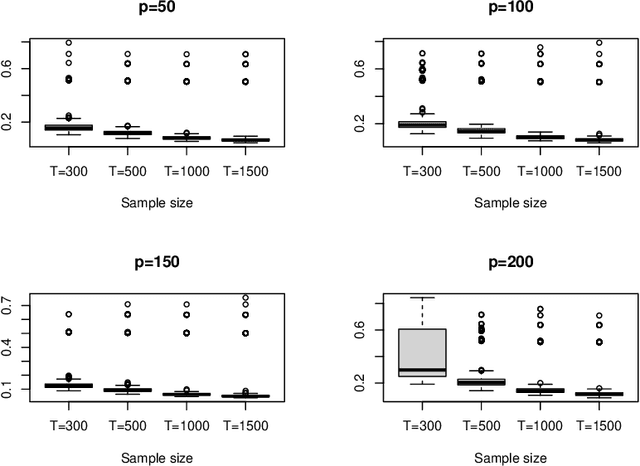
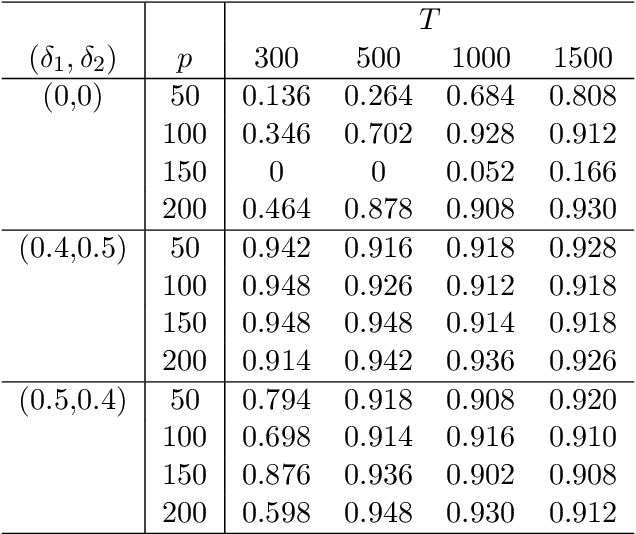
In this paper, we propose a distributed framework for reducing the dimensionality of high-dimensional, large-scale, heterogeneous matrix-variate time series data using a factor model. The data are first partitioned column-wise (or row-wise) and allocated to node servers, where each node estimates the row (or column) loading matrix via two-dimensional tensor PCA. These local estimates are then transmitted to a central server and aggregated, followed by a final PCA step to obtain the global row (or column) loading matrix estimator. Given the estimated loading matrices, the corresponding factor matrices are subsequently computed. Unlike existing distributed approaches, our framework preserves the latent matrix structure, thereby improving computational efficiency and enhancing information utilization. We also discuss row- and column-wise clustering procedures for settings in which the group memberships are unknown. Furthermore, we extend the analysis to unit-root nonstationary matrix-variate time series. Asymptotic properties of the proposed method are derived for the diverging dimension of the data in each computing unit and the sample size $T$. Simulation results assess the computational efficiency and estimation accuracy of the proposed framework, and real data applications further validate its predictive performance.

Modeling High-Dimensional Dependent Data in the Presence of Many Explanatory Variables and Weak Signals

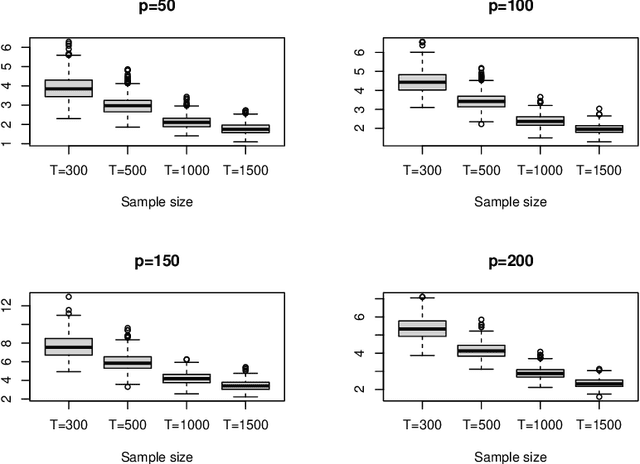
This article considers a novel and widely applicable approach to modeling high-dimensional dependent data when a large number of explanatory variables are available and the signal-to-noise ratio is low. We postulate that a $p$-dimensional response series is the sum of a linear regression with many observable explanatory variables and an error term driven by some latent common factors and an idiosyncratic noise. The common factors have dynamic dependence whereas the covariance matrix of the idiosyncratic noise can have diverging eigenvalues to handle the situation of low signal-to-noise ratio commonly encountered in applications. The regression coefficient matrix is estimated using penalized methods when the dimensions involved are high. We apply factor modeling to the regression residuals, employ a high-dimensional white noise testing procedure to determine the number of common factors, and adopt a projected Principal Component Analysis when the signal-to-noise ratio is low. We establish asymptotic properties of the proposed method, both for fixed and diverging numbers of regressors, as $p$ and the sample size $T$ approach infinity. Finally, we use simulations and empirical applications to demonstrate the efficacy of the proposed approach in finite samples.

Sparse Asymptotic PCA: Identifying Sparse Latent Factors Across Time Horizon

This paper proposes a novel method for sparse latent factor modeling using a new sparse asymptotic Principal Component Analysis (APCA). This approach analyzes the co-movements of large-dimensional panel data systems over time horizons within a general approximate factor model framework. Unlike existing sparse factor modeling approaches based on sparse PCA, which assume sparse loading matrices, our sparse APCA assumes that factor processes are sparse over the time horizon, while the corresponding loading matrices are not necessarily sparse. This development is motivated by the observation that the assumption of sparse loadings may not be appropriate for financial returns, where exposure to market factors is generally universal and non-sparse. We propose a truncated power method to estimate the first sparse factor process and a sequential deflation method for multi-factor cases. Additionally, we develop a data-driven approach to identify the sparsity of risk factors over the time horizon using a novel cross-sectional cross-validation method. Theoretically, we establish that our estimators are consistent under mild conditions. Monte Carlo simulations demonstrate that the proposed method performs well in finite samples. Empirically, we analyze daily stock returns for a balanced panel of S&P 500 stocks from January 2004 to December 2016. Through textual analysis, we examine specific events associated with the identified sparse factors that systematically influence the stock market. Our approach offers a new pathway for economists to study and understand the systematic risks of economic and financial systems over time.

Optimal Bias-Correction and Valid Inference in High-Dimensional Ridge Regression: A Closed-Form Solution

Ridge regression is an indispensable tool in big data econometrics but suffers from bias issues affecting both statistical efficiency and scalability. We introduce an iterative strategy to correct the bias effectively when the dimension $p$ is less than the sample size $n$. For $p>n$, our method optimally reduces the bias to a level unachievable through linear transformations of the response. We employ a Ridge-Screening (RS) method to handle the remaining bias when $p>n$, creating a reduced model suitable for bias-correction. Under certain conditions, the selected model nests the true one, making RS a novel variable selection approach. We establish the asymptotic properties and valid inferences of our de-biased ridge estimators for both $p< n$ and $p>n$, where $p$ and $n$ may grow towards infinity, along with the number of iterations. Our method is validated using simulated and real-world data examples, providing a closed-form solution to bias challenges in ridge regression inferences.