Modeling High-Dimensional Dependent Data in the Presence of Many Explanatory Variables and Weak Signals

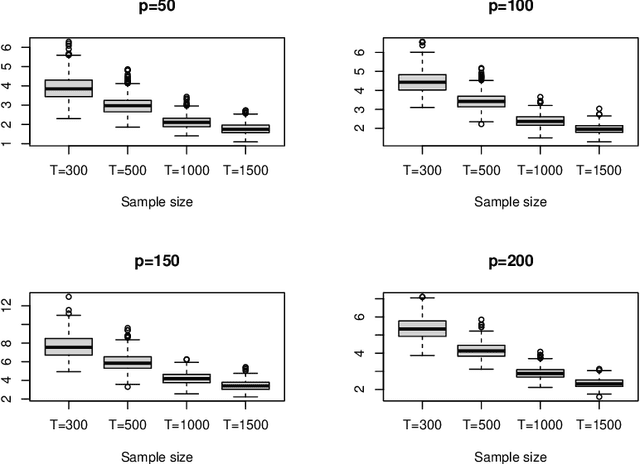
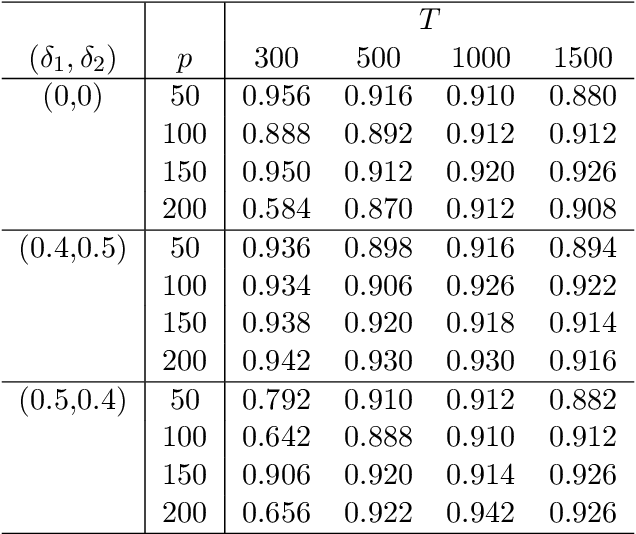
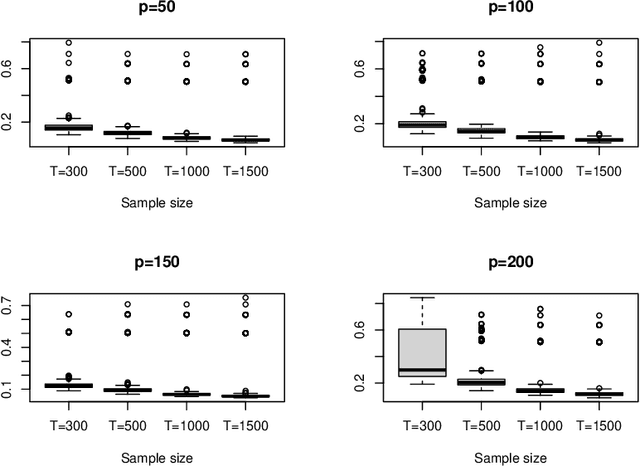
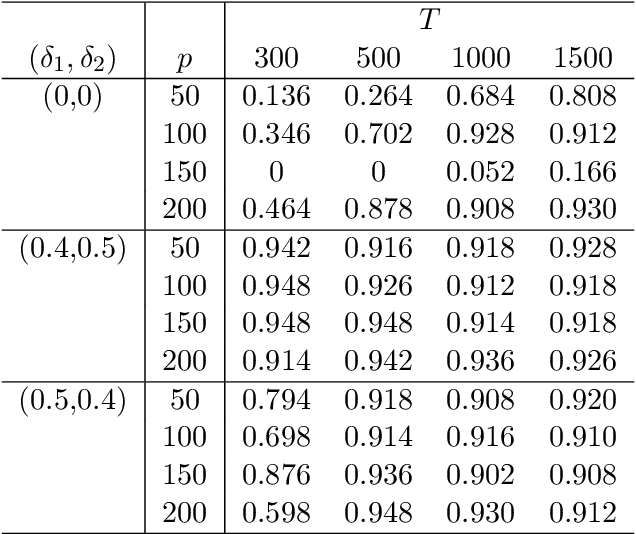
This article considers a novel and widely applicable approach to modeling high-dimensional dependent data when a large number of explanatory variables are available and the signal-to-noise ratio is low. We postulate that a $p$-dimensional response series is the sum of a linear regression with many observable explanatory variables and an error term driven by some latent common factors and an idiosyncratic noise. The common factors have dynamic dependence whereas the covariance matrix of the idiosyncratic noise can have diverging eigenvalues to handle the situation of low signal-to-noise ratio commonly encountered in applications. The regression coefficient matrix is estimated using penalized methods when the dimensions involved are high. We apply factor modeling to the regression residuals, employ a high-dimensional white noise testing procedure to determine the number of common factors, and adopt a projected Principal Component Analysis when the signal-to-noise ratio is low. We establish asymptotic properties of the proposed method, both for fixed and diverging numbers of regressors, as $p$ and the sample size $T$ approach infinity. Finally, we use simulations and empirical applications to demonstrate the efficacy of the proposed approach in finite samples.