Deep Learning Accelerated Quantum Transport Simulations in Nanoelectronics: From Break Junctions to Field-Effect Transistors

Quantum transport calculations are essential for understanding and designing nanoelectronic devices, yet the trade-off between accuracy and computational efficiency has long limited their practical applications. We present a general framework that combines the deep learning tight-binding Hamiltonian (DeePTB) approach with the non-equilibrium Green's Function (NEGF) method, enabling efficient quantum transport calculations while maintaining first-principles accuracy. We demonstrate the capabilities of the DeePTB-NEGF framework through two representative applications: comprehensive simulation of break junction systems, where conductance histograms show good agreement with experimental measurements in both metallic contact and single-molecule junction cases; and simulation of carbon nanotube field effect transistors through self-consistent NEGF-Poisson calculations, capturing essential physics including the electrostatic potential and transfer characteristic curves under finite bias conditions. This framework bridges the gap between first-principles accuracy and computational efficiency, providing a powerful tool for high-throughput quantum transport simulations across different scales in nanoelectronics.

Understanding Neural Networks with Logarithm Determinant Entropy Estimator

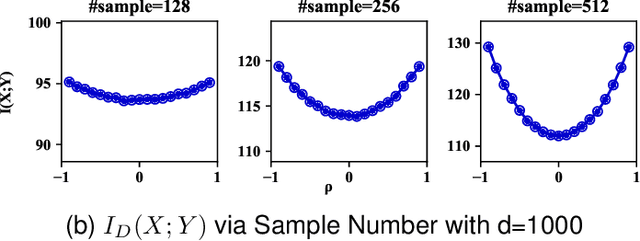
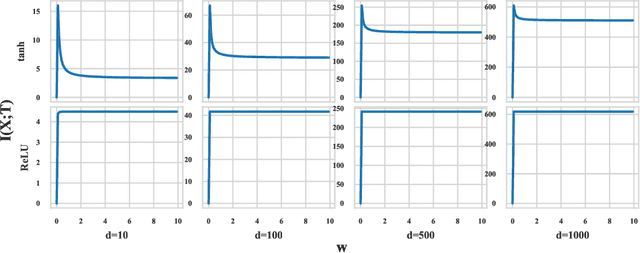
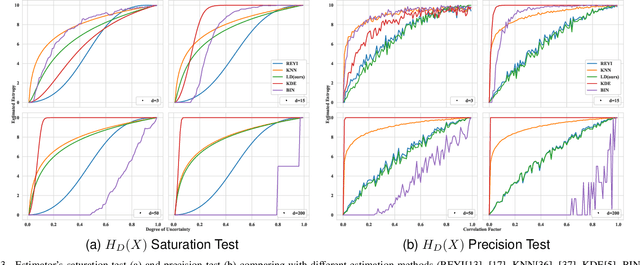
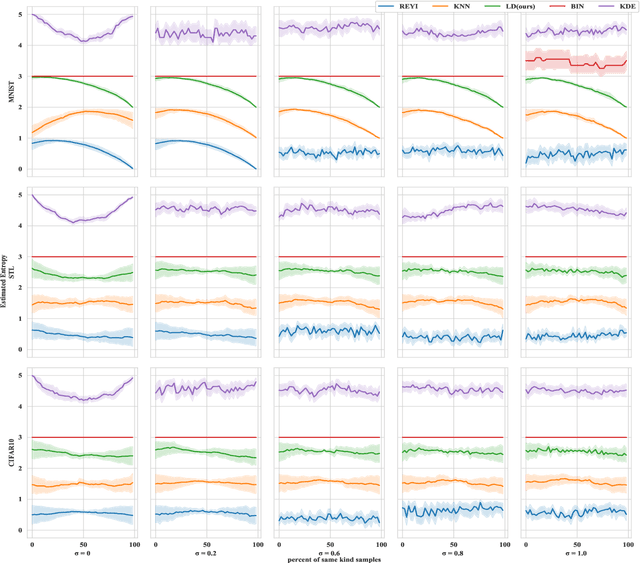
Understanding the informative behaviour of deep neural networks is challenged by misused estimators and the complexity of network structure, which leads to inconsistent observations and diversified interpretation. Here we propose the LogDet estimator -- a reliable matrix-based entropy estimator that approximates Shannon differential entropy. We construct informative measurements based on LogDet estimator, verify our method with comparable experiments and utilize it to analyse neural network behaviour. Our results demonstrate the LogDet estimator overcomes the drawbacks that emerge from highly diverse and degenerated distribution thus is reliable to estimate entropy in neural networks. The Network analysis results also find a functional distinction between shallow and deeper layers, which can help understand the compression phenomenon in the Information bottleneck theory of neural networks.