Variational Heteroscedastic Volatility Model

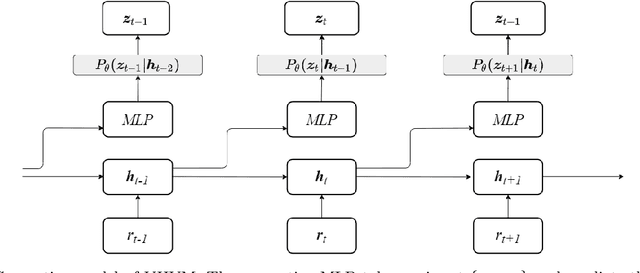
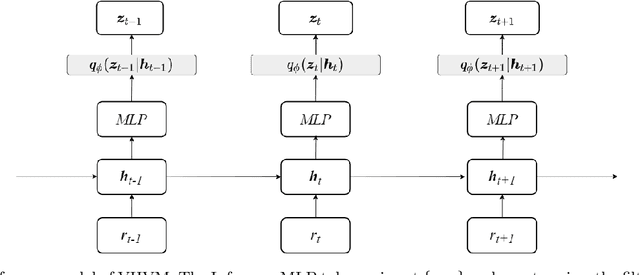
We propose Variational Heteroscedastic Volatility Model (VHVM) -- an end-to-end neural network architecture capable of modelling heteroscedastic behaviour in multivariate financial time series. VHVM leverages recent advances in several areas of deep learning, namely sequential modelling and representation learning, to model complex temporal dynamics between different asset returns. At its core, VHVM consists of a variational autoencoder to capture relationships between assets, and a recurrent neural network to model the time-evolution of these dependencies. The outputs of VHVM are time-varying conditional volatilities in the form of covariance matrices. We demonstrate the effectiveness of VHVM against existing methods such as Generalised AutoRegressive Conditional Heteroscedasticity (GARCH) and Stochastic Volatility (SV) models on a wide range of multivariate foreign currency (FX) datasets.

Deep Recurrent Modelling of Granger Causality with Latent Confounding

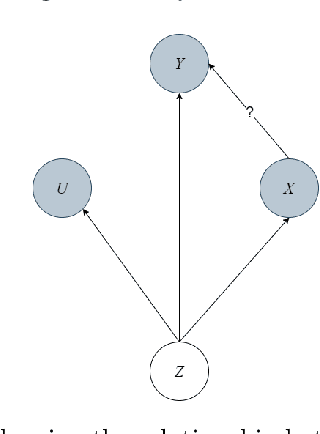
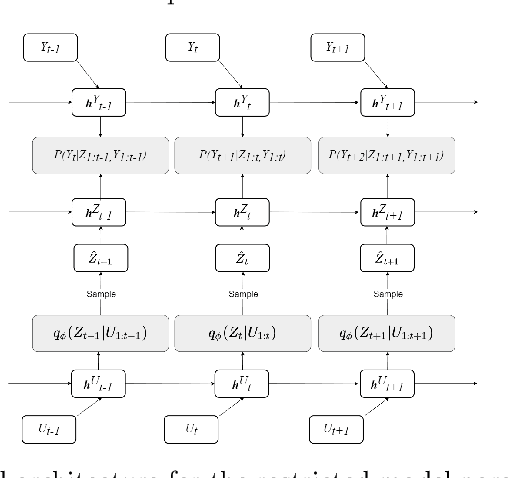
Inferring causal relationships in observational time series data is an important task when interventions cannot be performed. Granger causality is a popular framework to infer potential causal mechanisms between different time series. The original definition of Granger causality is restricted to linear processes and leads to spurious conclusions in the presence of a latent confounder. In this work, we harness the expressive power of recurrent neural networks and propose a deep learning-based approach to model non-linear Granger causality by directly accounting for latent confounders. Our approach leverages multiple recurrent neural networks to parameterise predictive distributions and we propose the novel use of a dual-decoder setup to conduct the Granger tests. We demonstrate the model performance on non-linear stochastic time series for which the latent confounder influences the cause and effect with different time lags; results show the effectiveness of our model compared to existing benchmarks.

Neural Generalised AutoRegressive Conditional Heteroskedasticity

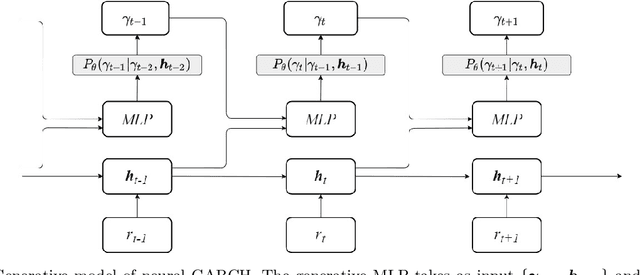
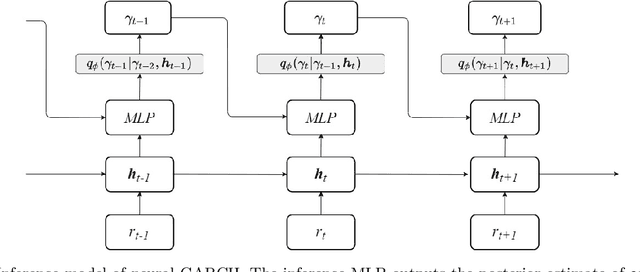
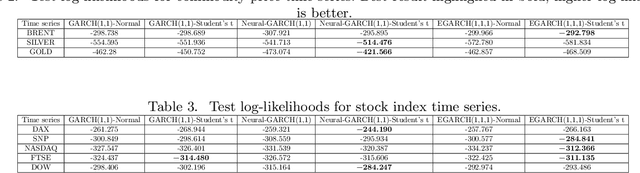
We propose Neural GARCH, a class of methods to model conditional heteroskedasticity in financial time series. Neural GARCH is a neural network adaptation of the GARCH 1,1 model in the univariate case, and the diagonal BEKK 1,1 model in the multivariate case. We allow the coefficients of a GARCH model to be time varying in order to reflect the constantly changing dynamics of financial markets. The time varying coefficients are parameterised by a recurrent neural network that is trained with stochastic gradient variational Bayes. We propose two variants of our model, one with normal innovations and the other with Students t innovations. We test our models on a wide range of univariate and multivariate financial time series, and we find that the Neural Students t model consistently outperforms the others.

Stochastic Recurrent Neural Network for Multistep Time Series Forecasting

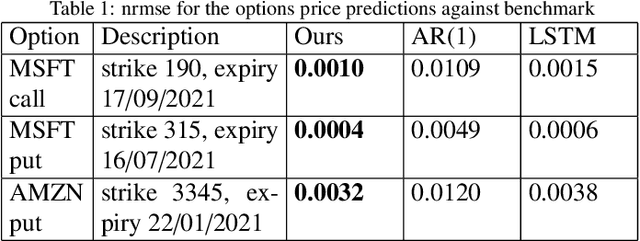
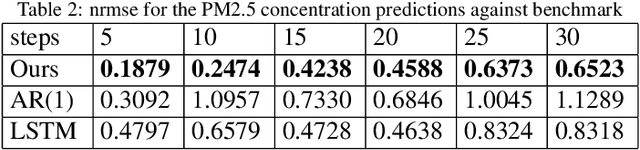
Time series forecasting based on deep architectures has been gaining popularity in recent years due to their ability to model complex non-linear temporal dynamics. The recurrent neural network is one such model capable of handling variable-length input and output. In this paper, we leverage recent advances in deep generative models and the concept of state space models to propose a stochastic adaptation of the recurrent neural network for multistep-ahead time series forecasting, which is trained with stochastic gradient variational Bayes. In our model design, the transition function of the recurrent neural network, which determines the evolution of the hidden states, is stochastic rather than deterministic as in a regular recurrent neural network; this is achieved by incorporating a latent random variable into the transition process which captures the stochasticity of the temporal dynamics. Our model preserves the architectural workings of a recurrent neural network for which all relevant information is encapsulated in its hidden states, and this flexibility allows our model to be easily integrated into any deep architecture for sequential modelling. We test our model on a wide range of datasets from finance to healthcare; results show that the stochastic recurrent neural network consistently outperforms its deterministic counterpart.