Neural Generalised AutoRegressive Conditional Heteroskedasticity
Paper and Code
Feb 23, 2022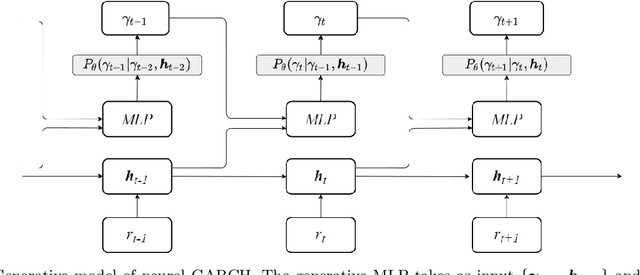

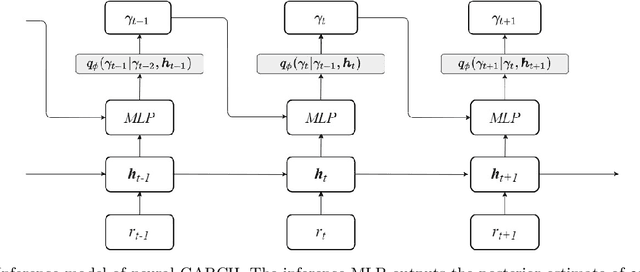
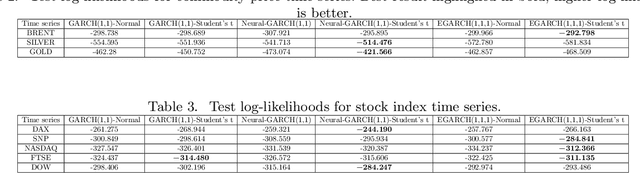
We propose Neural GARCH, a class of methods to model conditional heteroskedasticity in financial time series. Neural GARCH is a neural network adaptation of the GARCH 1,1 model in the univariate case, and the diagonal BEKK 1,1 model in the multivariate case. We allow the coefficients of a GARCH model to be time varying in order to reflect the constantly changing dynamics of financial markets. The time varying coefficients are parameterised by a recurrent neural network that is trained with stochastic gradient variational Bayes. We propose two variants of our model, one with normal innovations and the other with Students t innovations. We test our models on a wide range of univariate and multivariate financial time series, and we find that the Neural Students t model consistently outperforms the others.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge