Zexu Zhang
Probabilistic network topology prediction for active planning:An adaptive algorithm and application
Jun 27, 2022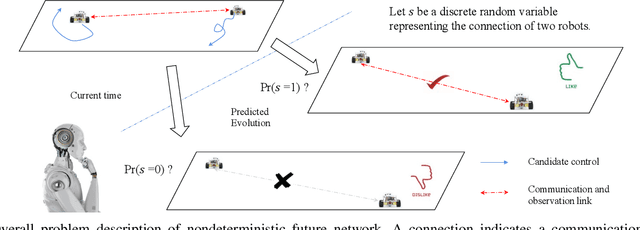
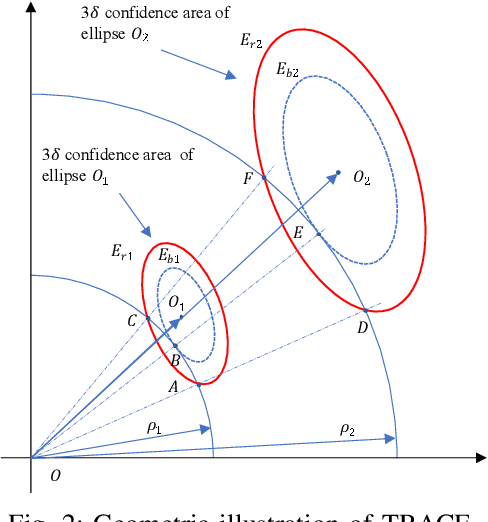

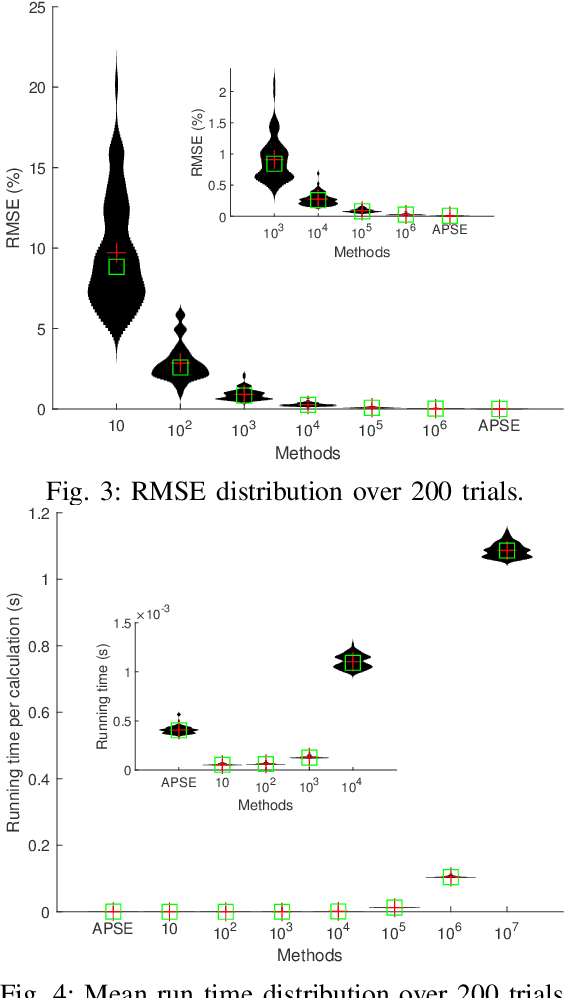
Abstract:This paper tackles the problem of active planning to achieve cooperative localization for multi-robot systems (MRS) under measurement uncertainty in GNSS-limited scenarios. Specifically, we address the issue of accurately predicting the probability of a future connection between two robots equipped with range-based measurement devices. Due to the limited range of the equipped sensors, edges in the network connection topology will be created or destroyed as the robots move with respect to one another. Accurately predicting the future existence of an edge, given imperfect state estimation and noisy actuation, is therefore a challenging task. An adaptive power series expansion (or APSE) algorithm is developed based on current estimates and control candidates. Such an algorithm applies the power series expansion formula of the quadratic positive form in a normal distribution. Finite-term approximation is made to realize the computational tractability. Further analyses are presented to show that the truncation error in the finite-term approximation can be theoretically reduced to a desired threshold by adaptively choosing the summation degree of the power series. Several sufficient conditions are rigorously derived as the selection principles. Finally, extensive simulation results and comparisons, with respect to both single and multi-robot cases, validate that a formally computed and therefore more accurate probability of future topology can help improve the performance of active planning under uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge