Cell division in deep material networks applied to multiscale strain localization modeling

Despite the increasing importance of strain localization modeling (e.g., failure analysis) in computer-aided engineering, there is a lack of effective approaches to consistently modeling related material behaviors across multiple length scales. We aim to address this gap within the framework of deep material networks (DMN) - a physics-based machine learning model with embedded mechanics in the building blocks. A new cell division scheme is proposed to track the scale transition through the network, and its consistency is ensured by the physics of fitting parameters. Essentially, each microscale node in the bottom layer is described by an ellipsoidal cell with its dimensions back-propagated from the macroscale material point. New crack surfaces in the cell are modeled by enriching cohesive layers, and failure algorithms are developed for crack initiation and evolution in the implicit DMN analysis. Besides single material point studies, we apply the multiscale model to concurrent multiscale simulations for the dynamic crush of a particle-reinforced composite tube and various tests on carbon fiber reinforced polymer composites. For the latter, experimental validations on an off-axis tensile test specimen are also provided.

Machine learning for metal additive manufacturing: Predicting temperature and melt pool fluid dynamics using physics-informed neural networks

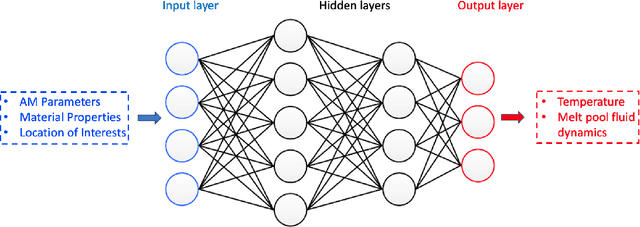
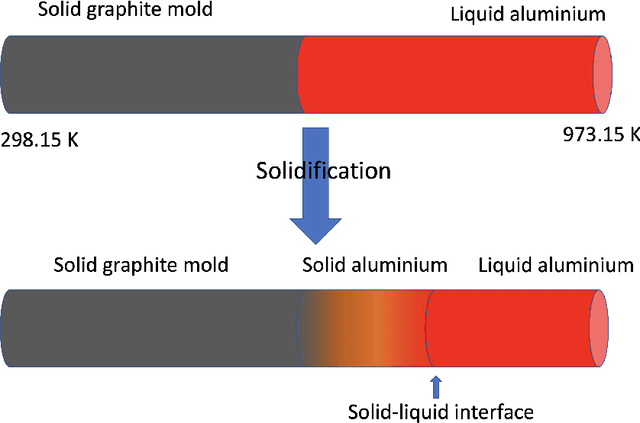
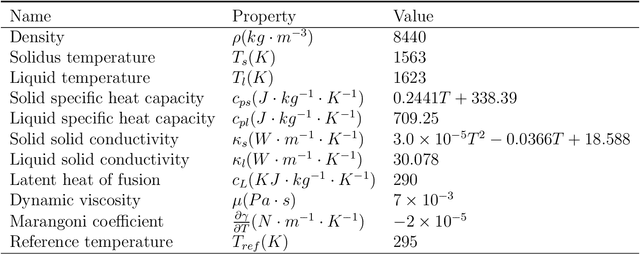
The recent explosion of machine learning (ML) and artificial intelligence (AI) shows great potential in the breakthrough of metal additive manufacturing (AM) process modeling. However, the success of conventional machine learning tools in data science is primarily attributed to the unprecedented large amount of labeled data-sets (big data), which can be either obtained by experiments or first-principle simulations. Unfortunately, these labeled data-sets are expensive to obtain in AM due to the high expense of the AM experiments and prohibitive computational cost of high-fidelity simulations. We propose a physics-informed neural network (PINN) framework that fuses both data and first physical principles, including conservation laws of momentum, mass, and energy, into the neural network to inform the learning processes. To the best knowledge of the authors, this is the first application of PINN to three dimensional AM processes modeling. Besides, we propose a hard-type approach for Dirichlet boundary conditions (BCs) based on a Heaviside function, which can not only enforce the BCs but also accelerate the learning process. The PINN framework is applied to two representative metal manufacturing problems, including the 2018 NIST AM-Benchmark test series. We carefully assess the performance of the PINN model by comparing the predictions with available experimental data and high-fidelity simulation results. The investigations show that the PINN, owed to the additional physical knowledge, can accurately predict the temperature and melt pool dynamics during metal AM processes with only a moderate amount of labeled data-sets. The foray of PINN to metal AM shows the great potential of physics-informed deep learning for broader applications to advanced manufacturing.

Intelligent multiscale simulation based on process-guided composite database

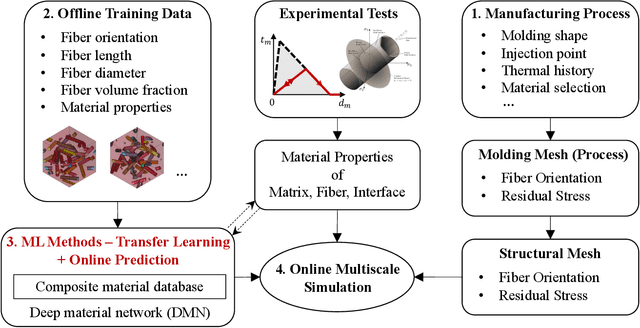
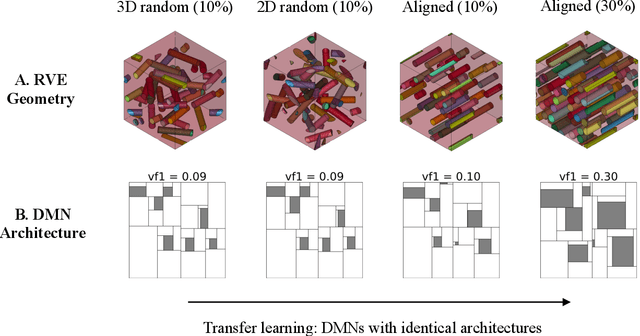
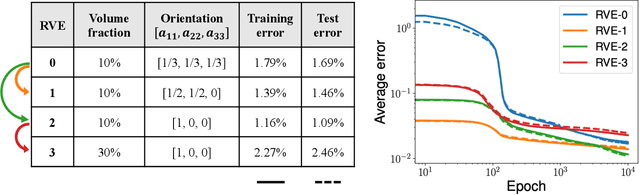
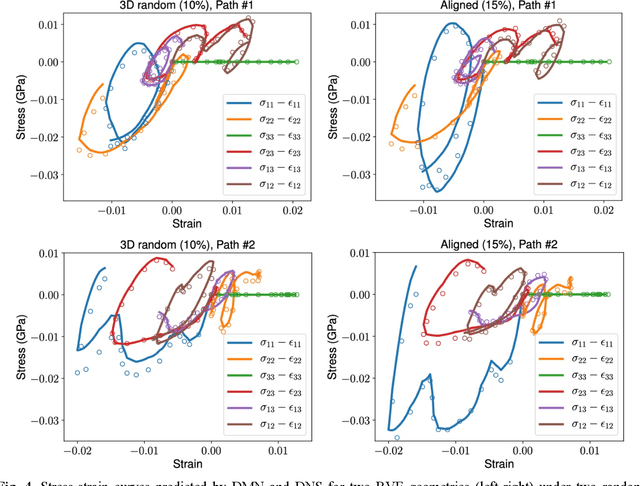
In the paper, we present an integrated data-driven modeling framework based on process modeling, material homogenization, mechanistic machine learning, and concurrent multiscale simulation. We are interested in the injection-molded short fiber reinforced composites, which have been identified as key material systems in automotive, aerospace, and electronics industries. The molding process induces spatially varying microstructures across various length scales, while the resulting strongly anisotropic and nonlinear material properties are still challenging to be captured by conventional modeling approaches. To prepare the linear elastic training data for our machine learning tasks, Representative Volume Elements (RVE) with different fiber orientations and volume fractions are generated through stochastic reconstruction. More importantly, we utilize the recently proposed Deep Material Network (DMN) to learn the hidden microscale morphologies from data. With essential physics embedded in its building blocks, this data-driven material model can be extrapolated to predict nonlinear material behaviors efficiently and accurately. Through the transfer learning of DMN, we create a unified process-guided material database that covers a full range of geometric descriptors for short fiber reinforced composites. Finally, this unified DMN database is implemented and coupled with macroscale finite element model to enable concurrent multiscale simulations. From our perspective, the proposed framework is also promising in many other emergent multiscale engineering systems, such as additive manufacturing and compressive molding.

Deep material network with cohesive layers: Multi-stage training and interfacial failure analysis

A fundamental issue in multiscale materials modeling and design is the consideration of traction-separation behavior at the interface, which generally influences the failure properties. This paper develops a physics-based machine learning model based on the deep material network (DMN) enriched by cohesive layers, which enables the accurate and efficient prediction of multiscale responses for heterogeneous materials with interfacial effect. New fitting parameters are invoked in the cohesive building block and have physical meanings related to the length scale and orientation of the cohesive layer. It is shown that the enriched material network can be effectively optimized via a multi-stage training strategy, with training data generated from linear elastic direct numerical simulation (DNS). The extrapolation capability of the method to unknown spaces is demonstrated through the debonding analysis of a unidirectional fiber-reinforced composite, where the interface behavior is governed by an irreversible softening mixed-mode cohesive law. Its predictive accuracy is validated against the nonlinear DNS results, and the reduction in computational time is particularly significant.

Exploring the 3D architectures of deep material network in data-driven multiscale mechanics

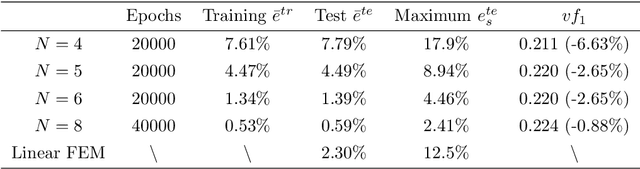
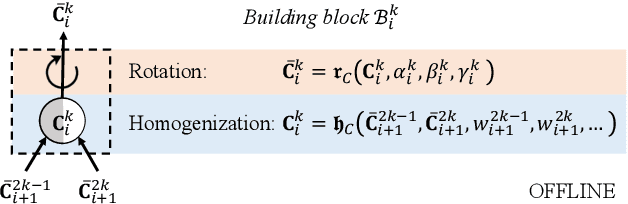
This paper extends the deep material network (DMN) proposed by Liu et al. (2018) to tackle general 3-dimensional (3D) problems with arbitrary material and geometric nonlinearities. The global framework of DMN for mechanistic data-driven multiscale material modeling is discussed in detail on the offline training and online extrapolation stages. Analytical solutions of the 3D building block with a two-layer structure in both small- and finite-strain formulations are derived based on interfacial equilibrium conditions and kinematic constraints. With linear elastic data generated by direct numerical simulations on a representative volume element (RVE), the network can be effectively trained in offline stage using stochastic gradient descent and advanced model compression algorithms. Efficiency and accuracy of DMN on addressing the long-standing 3D RVE challenges with complex morphologies and material laws are validated through numerical experiments, including 1) hyperelastic particle-reinforced rubber composite with Mullins effect; 2) polycrystalline materials with rate-dependent crystal plasticity; 3) carbon fiber reinforced polymer (CFRP) composites with fiber anisotropic elasticity and matrix plasticity. In particular, we demonstrate a three-scale homogenization procedure of CFRP system by concatenating the microscale and mesoscale material networks. The complete learning and extrapolation procedures of DMN establish a reliable data-driven framework for multiscale material modeling and design.