Test-time Controllable Image Generation by Explicit Spatial Constraint Enforcement

Recent text-to-image generation favors various forms of spatial conditions, e.g., masks, bounding boxes, and key points. However, the majority of the prior art requires form-specific annotations to fine-tune the original model, leading to poor test-time generalizability. Meanwhile, existing training-free methods work well only with simplified prompts and spatial conditions. In this work, we propose a novel yet generic test-time controllable generation method that aims at natural text prompts and complex conditions. Specifically, we decouple spatial conditions into semantic and geometric conditions and then enforce their consistency during the image-generation process individually. As for the former, we target bridging the gap between the semantic condition and text prompts, as well as the gap between such condition and the attention map from diffusion models. To achieve this, we propose to first complete the prompt w.r.t. semantic condition, and then remove the negative impact of distracting prompt words by measuring their statistics in attention maps as well as distances in word space w.r.t. this condition. To further cope with the complex geometric conditions, we introduce a geometric transform module, in which Region-of-Interests will be identified in attention maps and further used to translate category-wise latents w.r.t. geometric condition. More importantly, we propose a diffusion-based latents-refill method to explicitly remove the impact of latents at the RoI, reducing the artifacts on generated images. Experiments on Coco-stuff dataset showcase 30$\%$ relative boost compared to SOTA training-free methods on layout consistency evaluation metrics.

Observation of high-energy neutrinos from the Galactic plane

The origin of high-energy cosmic rays, atomic nuclei that continuously impact Earth's atmosphere, has been a mystery for over a century. Due to deflection in interstellar magnetic fields, cosmic rays from the Milky Way arrive at Earth from random directions. However, near their sources and during propagation, cosmic rays interact with matter and produce high-energy neutrinos. We search for neutrino emission using machine learning techniques applied to ten years of data from the IceCube Neutrino Observatory. We identify neutrino emission from the Galactic plane at the 4.5$\sigma$ level of significance, by comparing diffuse emission models to a background-only hypothesis. The signal is consistent with modeled diffuse emission from the Galactic plane, but could also arise from a population of unresolved point sources.

Graph Neural Networks for Low-Energy Event Classification & Reconstruction in IceCube

IceCube, a cubic-kilometer array of optical sensors built to detect atmospheric and astrophysical neutrinos between 1 GeV and 1 PeV, is deployed 1.45 km to 2.45 km below the surface of the ice sheet at the South Pole. The classification and reconstruction of events from the in-ice detectors play a central role in the analysis of data from IceCube. Reconstructing and classifying events is a challenge due to the irregular detector geometry, inhomogeneous scattering and absorption of light in the ice and, below 100 GeV, the relatively low number of signal photons produced per event. To address this challenge, it is possible to represent IceCube events as point cloud graphs and use a Graph Neural Network (GNN) as the classification and reconstruction method. The GNN is capable of distinguishing neutrino events from cosmic-ray backgrounds, classifying different neutrino event types, and reconstructing the deposited energy, direction and interaction vertex. Based on simulation, we provide a comparison in the 1-100 GeV energy range to the current state-of-the-art maximum likelihood techniques used in current IceCube analyses, including the effects of known systematic uncertainties. For neutrino event classification, the GNN increases the signal efficiency by 18% at a fixed false positive rate (FPR), compared to current IceCube methods. Alternatively, the GNN offers a reduction of the FPR by over a factor 8 (to below half a percent) at a fixed signal efficiency. For the reconstruction of energy, direction, and interaction vertex, the resolution improves by an average of 13%-20% compared to current maximum likelihood techniques in the energy range of 1-30 GeV. The GNN, when run on a GPU, is capable of processing IceCube events at a rate nearly double of the median IceCube trigger rate of 2.7 kHz, which opens the possibility of using low energy neutrinos in online searches for transient events.

The Dark Machines Anomaly Score Challenge: Benchmark Data and Model Independent Event Classification for the Large Hadron Collider

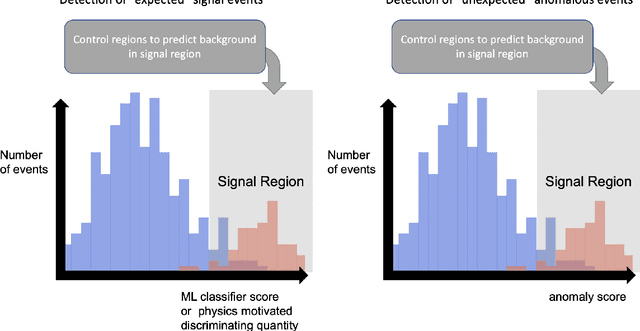
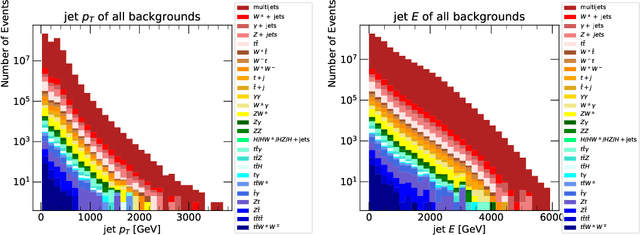
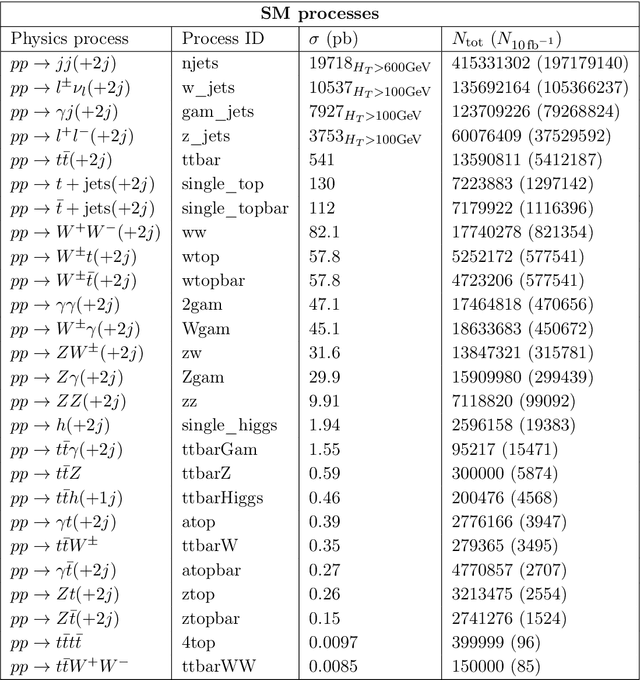
We describe the outcome of a data challenge conducted as part of the Dark Machines Initiative and the Les Houches 2019 workshop on Physics at TeV colliders. The challenged aims at detecting signals of new physics at the LHC using unsupervised machine learning algorithms. First, we propose how an anomaly score could be implemented to define model-independent signal regions in LHC searches. We define and describe a large benchmark dataset, consisting of >1 Billion simulated LHC events corresponding to $10~\rm{fb}^{-1}$ of proton-proton collisions at a center-of-mass energy of 13 TeV. We then review a wide range of anomaly detection and density estimation algorithms, developed in the context of the data challenge, and we measure their performance in a set of realistic analysis environments. We draw a number of useful conclusions that will aid the development of unsupervised new physics searches during the third run of the LHC, and provide our benchmark dataset for future studies at https://www.phenoMLdata.org. Code to reproduce the analysis is provided at https://github.com/bostdiek/DarkMachines-UnsupervisedChallenge.

A Convolutional Neural Network based Cascade Reconstruction for the IceCube Neutrino Observatory

Continued improvements on existing reconstruction methods are vital to the success of high-energy physics experiments, such as the IceCube Neutrino Observatory. In IceCube, further challenges arise as the detector is situated at the geographic South Pole where computational resources are limited. However, to perform real-time analyses and to issue alerts to telescopes around the world, powerful and fast reconstruction methods are desired. Deep neural networks can be extremely powerful, and their usage is computationally inexpensive once the networks are trained. These characteristics make a deep learning-based approach an excellent candidate for the application in IceCube. A reconstruction method based on convolutional architectures and hexagonally shaped kernels is presented. The presented method is robust towards systematic uncertainties in the simulation and has been tested on experimental data. In comparison to standard reconstruction methods in IceCube, it can improve upon the reconstruction accuracy, while reducing the time necessary to run the reconstruction by two to three orders of magnitude.

Variational Physics-Informed Neural Networks For Solving Partial Differential Equations

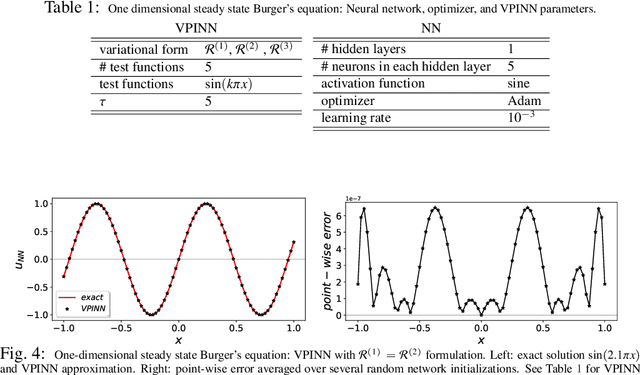
Physics-informed neural networks (PINNs) [31] use automatic differentiation to solve partial differential equations (PDEs) by penalizing the PDE in the loss function at a random set of points in the domain of interest. Here, we develop a Petrov-Galerkin version of PINNs based on the nonlinear approximation of deep neural networks (DNNs) by selecting the {\em trial space} to be the space of neural networks and the {\em test space} to be the space of Legendre polynomials. We formulate the \textit{variational residual} of the PDE using the DNN approximation by incorporating the variational form of the problem into the loss function of the network and construct a \textit{variational physics-informed neural network} (VPINN). By integrating by parts the integrand in the variational form, we lower the order of the differential operators represented by the neural networks, hence effectively reducing the training cost in VPINNs while increasing their accuracy compared to PINNs that essentially employ delta test functions. For shallow networks with one hidden layer, we analytically obtain explicit forms of the \textit{variational residual}. We demonstrate the performance of the new formulation for several examples that show clear advantages of VPINNs over PINNs in terms of both accuracy and speed.

Blind Ptychography by Douglas-Rachford Splitting

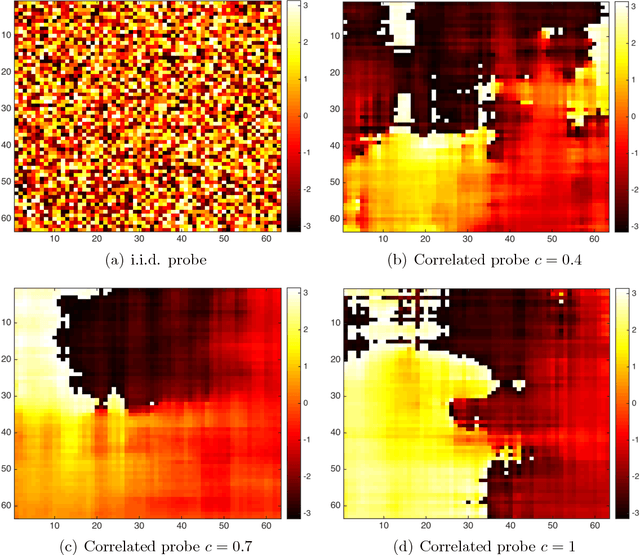
Blind ptychography is the scanning version of coherent diffractive imaging which seeks to recover both the object and the probe simultaneously. Based on alternating minimization by Douglas-Rachford splitting, AMDRS is a blind ptychographic algorithm informed by the uniqueness theory, the Poisson noise model and the stability analysis. Enhanced by the initialization method and the use of a randomly phased mask, AMDRS converges globally and geometrically. Three boundary conditions are considered in the simulations: periodic, dark-field and bright-field boundary conditions. The dark-field boundary condition is suited for isolated objects while the bright-field boundary condition is for non-isolated objects. The periodic boundary condition is a mathematically convenient reference point. Depending on the avail- ability of the boundary prior the dark-field and the bright-field boundary conditions may or may not be enforced in the reconstruction. Not surprisingly, enforcing the boundary condition improves the rate of convergence, sometimes in a significant way. Enforcing the bright-field condition in the reconstruction can also remove the linear phase ambiguity.

Efficient Multiscale Gaussian Process Regression using Hierarchical Clustering

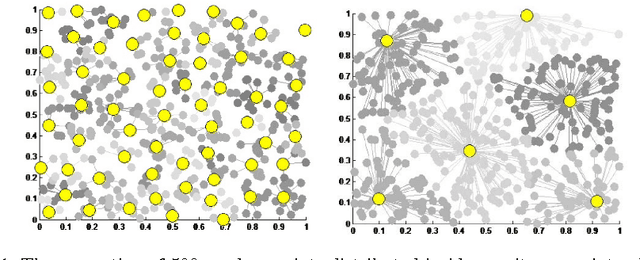
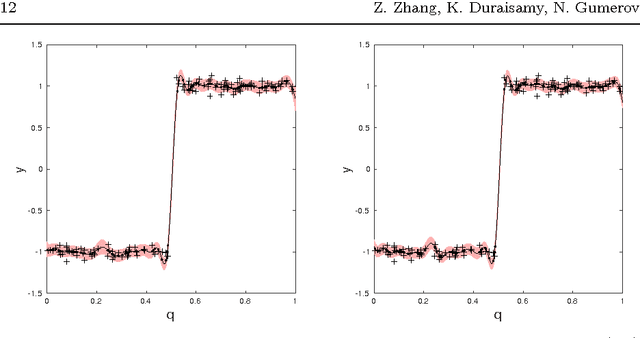
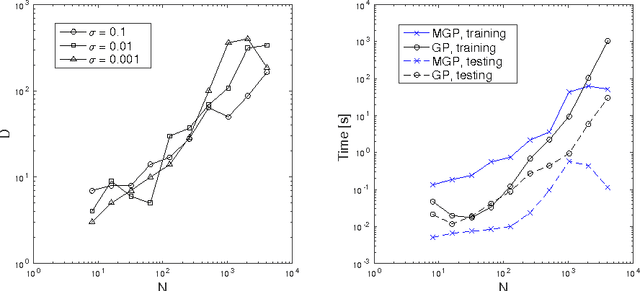
Standard Gaussian Process (GP) regression, a powerful machine learning tool, is computationally expensive when it is applied to large datasets, and potentially inaccurate when data points are sparsely distributed in a high-dimensional feature space. To address these challenges, a new multiscale, sparsified GP algorithm is formulated, with the goal of application to large scientific computing datasets. In this approach, the data is partitioned into clusters and the cluster centers are used to define a reduced training set, resulting in an improvement over standard GPs in terms of training and evaluation costs. Further, a hierarchical technique is used to adaptively map the local covariance representation to the underlying sparsity of the feature space, leading to improved prediction accuracy when the data distribution is highly non-uniform. A theoretical investigation of the computational complexity of the algorithm is presented. The efficacy of this method is then demonstrated on smooth and discontinuous analytical functions and on data from a direct numerical simulation of turbulent combustion.