N. A. Gumerov
Efficient Multiscale Gaussian Process Regression using Hierarchical Clustering
Mar 07, 2016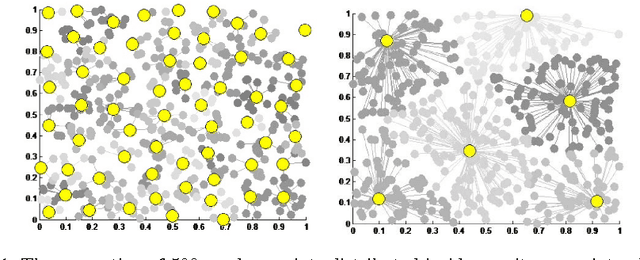

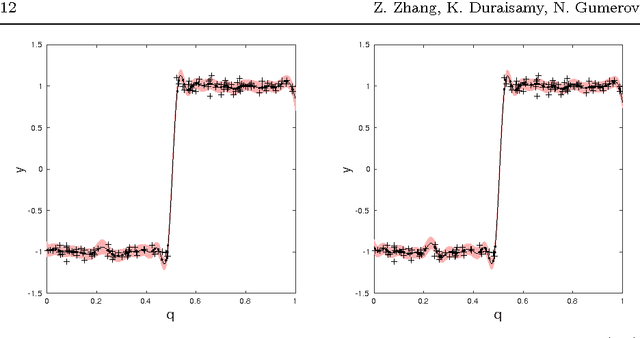
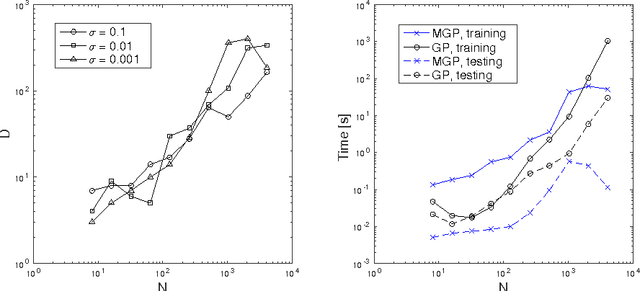
Abstract:Standard Gaussian Process (GP) regression, a powerful machine learning tool, is computationally expensive when it is applied to large datasets, and potentially inaccurate when data points are sparsely distributed in a high-dimensional feature space. To address these challenges, a new multiscale, sparsified GP algorithm is formulated, with the goal of application to large scientific computing datasets. In this approach, the data is partitioned into clusters and the cluster centers are used to define a reduced training set, resulting in an improvement over standard GPs in terms of training and evaluation costs. Further, a hierarchical technique is used to adaptively map the local covariance representation to the underlying sparsity of the feature space, leading to improved prediction accuracy when the data distribution is highly non-uniform. A theoretical investigation of the computational complexity of the algorithm is presented. The efficacy of this method is then demonstrated on smooth and discontinuous analytical functions and on data from a direct numerical simulation of turbulent combustion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge