A Mamba Foundation Model for Time Series Forecasting

Time series foundation models have demonstrated strong performance in zero-shot learning, making them well-suited for predicting rapidly evolving patterns in real-world applications where relevant training data are scarce. However, most of these models rely on the Transformer architecture, which incurs quadratic complexity as input length increases. To address this, we introduce TSMamba, a linear-complexity foundation model for time series forecasting built on the Mamba architecture. The model captures temporal dependencies through both forward and backward Mamba encoders, achieving high prediction accuracy. To reduce reliance on large datasets and lower training costs, TSMamba employs a two-stage transfer learning process that leverages pretrained Mamba LLMs, allowing effective time series modeling with a moderate training set. In the first stage, the forward and backward backbones are optimized via patch-wise autoregressive prediction; in the second stage, the model trains a prediction head and refines other components for long-term forecasting. While the backbone assumes channel independence to manage varying channel numbers across datasets, a channel-wise compressed attention module is introduced to capture cross-channel dependencies during fine-tuning on specific multivariate datasets. Experiments show that TSMamba's zero-shot performance is comparable to state-of-the-art time series foundation models, despite using significantly less training data. It also achieves competitive or superior full-shot performance compared to task-specific prediction models. The code will be made publicly available.

A Joint Time-frequency Domain Transformer for Multivariate Time Series Forecasting

To enhance predicting performance while minimizing computational demands, this paper introduces a joint time-frequency domain Transformer (JTFT) for multivariate forecasting. The method exploits the sparsity of time series in the frequency domain using a small number of learnable frequencies to extract temporal dependencies effectively. Alongside the frequency domain representation, a fixed number of the most recent data points are directly encoded in the time domain, bolstering the learning of local relationships and mitigating the adverse effects of non-stationarity. JTFT achieves linear complexity since the length of the internal representation remains independent of the input sequence length. Additionally, a low-rank attention layer is proposed to efficiently capture cross-dimensional dependencies and prevent performance degradation due to the entanglement of temporal and channel-wise modeling. Experiments conducted on six real-world datasets demonstrate that JTFT outperforms state-of-the-art methods.

NAMSG: An Efficient Method For Training Neural Networks

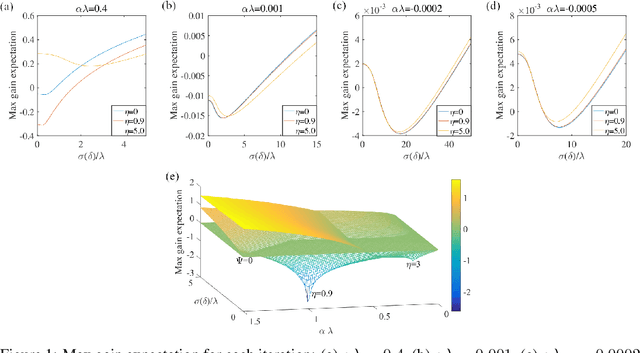
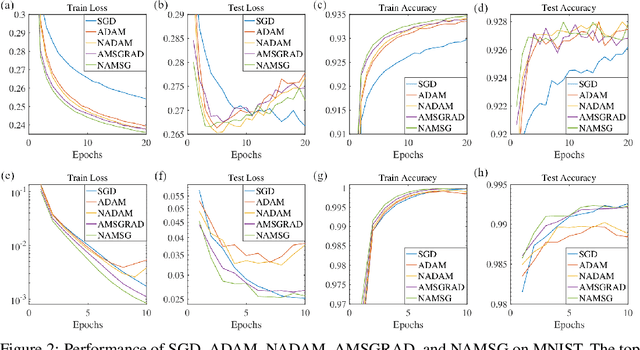
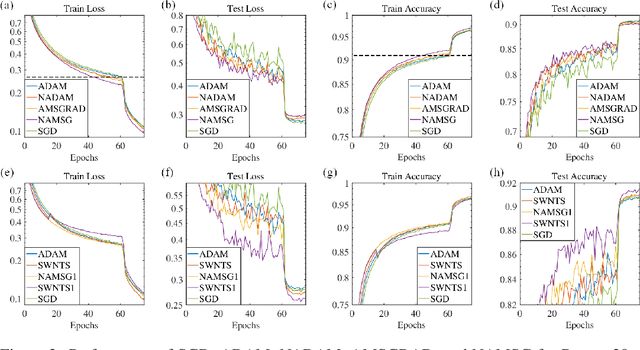
We introduce NAMSG, an adaptive first-order algorithm for training neural networks. The method is efficient in computation and memory, and is straightforward to implement. It computes the gradients at configurable remote observation points, in order to expedite the convergence by adjusting the step size for directions with different curvatures in the stochastic setting. It also scales the updating vector elementwise by a nonincreasing preconditioner to take the advantages of AMSGRAD. We analyze the convergence properties for both convex and nonconvex problems by modeling the training process as a dynamic system, and provide a guideline to select the observation distance without grid search. A data-dependent regret bound is proposed to guarantee the convergence in the convex setting. Experiments demonstrate that NAMSG works well in practical problems and compares favorably to popular adaptive methods, such as ADAM, NADAM, and AMSGRAD.