NAMSG: An Efficient Method For Training Neural Networks

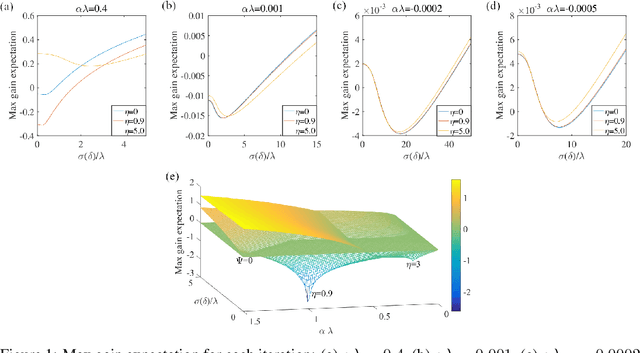
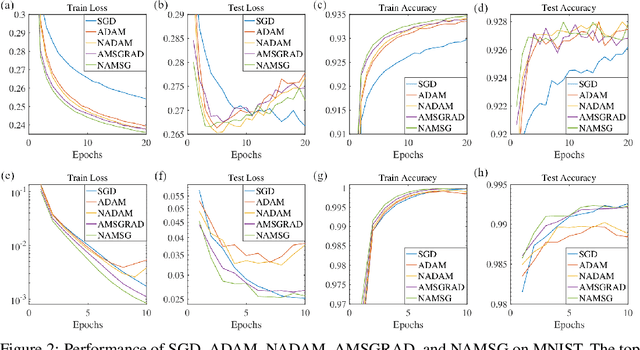
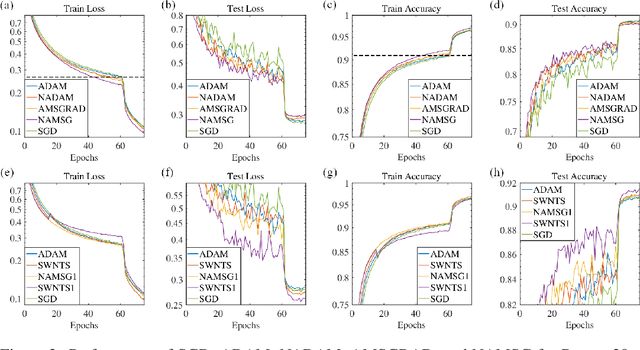
We introduce NAMSG, an adaptive first-order algorithm for training neural networks. The method is efficient in computation and memory, and is straightforward to implement. It computes the gradients at configurable remote observation points, in order to expedite the convergence by adjusting the step size for directions with different curvatures in the stochastic setting. It also scales the updating vector elementwise by a nonincreasing preconditioner to take the advantages of AMSGRAD. We analyze the convergence properties for both convex and nonconvex problems by modeling the training process as a dynamic system, and provide a guideline to select the observation distance without grid search. A data-dependent regret bound is proposed to guarantee the convergence in the convex setting. Experiments demonstrate that NAMSG works well in practical problems and compares favorably to popular adaptive methods, such as ADAM, NADAM, and AMSGRAD.