Differentially Private Covariate Balancing Causal Inference

Differential privacy is the leading mathematical framework for privacy protection, providing a probabilistic guarantee that safeguards individuals' private information when publishing statistics from a dataset. This guarantee is achieved by applying a randomized algorithm to the original data, which introduces unique challenges in data analysis by distorting inherent patterns. In particular, causal inference using observational data in privacy-sensitive contexts is challenging because it requires covariate balance between treatment groups, yet checking the true covariates is prohibited to prevent leakage of sensitive information. In this article, we present a differentially private two-stage covariate balancing weighting estimator to infer causal effects from observational data. Our algorithm produces both point and interval estimators with statistical guarantees, such as consistency and rate optimality, under a given privacy budget.

Novel Change of Measure Inequalities and PAC-Bayesian Bounds

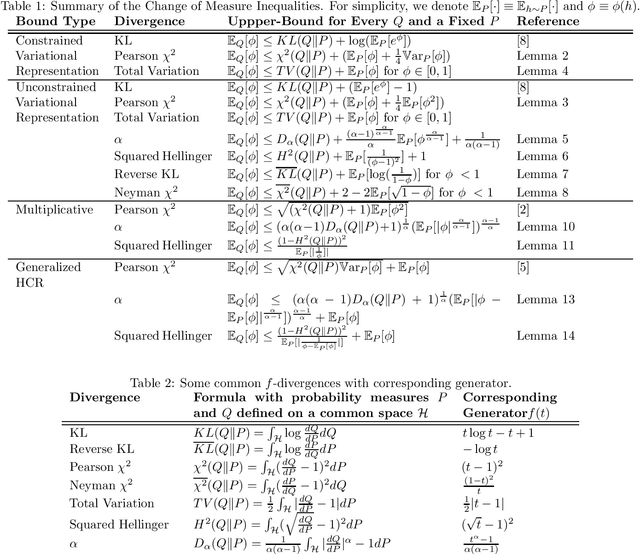
PAC-Bayesian theory has received a growing attention in the machine learning community. Our work extends the PAC-Bayesian theory by introducing several novel change of measure inequalities for two families of divergences: $f$-divergences and $\alpha$-divergences. First, we show how the variational representation for $f$-divergences leads to novel change of measure inequalities. Second, we propose a multiplicative change of measure inequality for $\alpha$-divergences, which leads to tighter bounds under some technical conditions. Finally, we present several PAC-Bayesian bounds for various classes of random variables, by using our novel change of measure inequalities.