Novel Change of Measure Inequalities and PAC-Bayesian Bounds
Paper and Code
Feb 25, 2020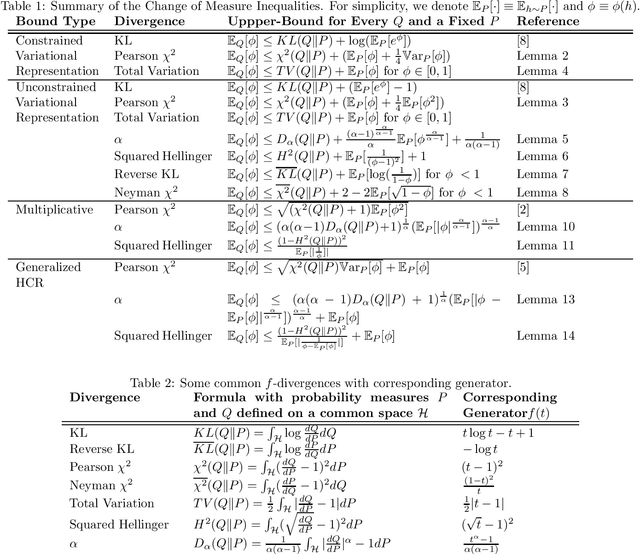
PAC-Bayesian theory has received a growing attention in the machine learning community. Our work extends the PAC-Bayesian theory by introducing several novel change of measure inequalities for two families of divergences: $f$-divergences and $\alpha$-divergences. First, we show how the variational representation for $f$-divergences leads to novel change of measure inequalities. Second, we propose a multiplicative change of measure inequality for $\alpha$-divergences, which leads to tighter bounds under some technical conditions. Finally, we present several PAC-Bayesian bounds for various classes of random variables, by using our novel change of measure inequalities.
* 9 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge