Unsupervised Learning in Echo State Networks for Input Reconstruction

Conventional echo state networks (ESNs) require supervised learning to train the readout layer, using the desired outputs as training data. In this study, we focus on input reconstruction (IR), which refers to training the readout layer to reproduce the input time series in its output. We reformulate the learning algorithm of the ESN readout layer to perform IR using unsupervised learning (UL). By conducting theoretical analysis and numerical experiments, we demonstrate that IR in ESNs can be effectively implemented under realistic conditions without explicitly using the desired outputs as training data; in this way, UL is enabled. Furthermore, we demonstrate that applications relying on IR, such as dynamical system replication and noise filtering, can be reformulated within the UL framework. Our findings establish a theoretically sound and universally applicable IR formulation, along with its related tasks in ESNs. This work paves the way for novel predictions and highlights unresolved theoretical challenges in ESNs, particularly in the context of time-series processing methods and computational models of the brain.

Prediction of Unobserved Bifurcation by Unsupervised Extraction of Slowly Time-Varying System Parameter Dynamics from Time Series Using Reservoir Computing

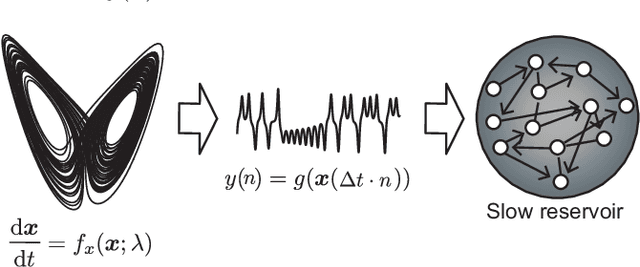
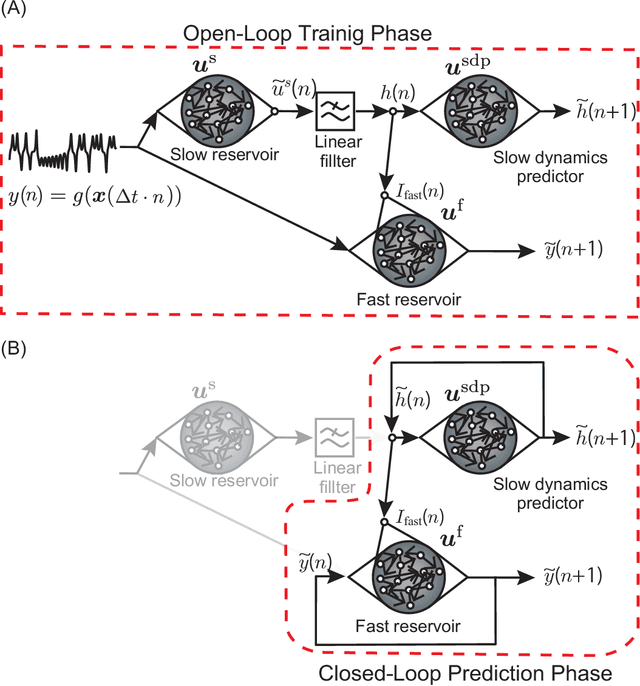
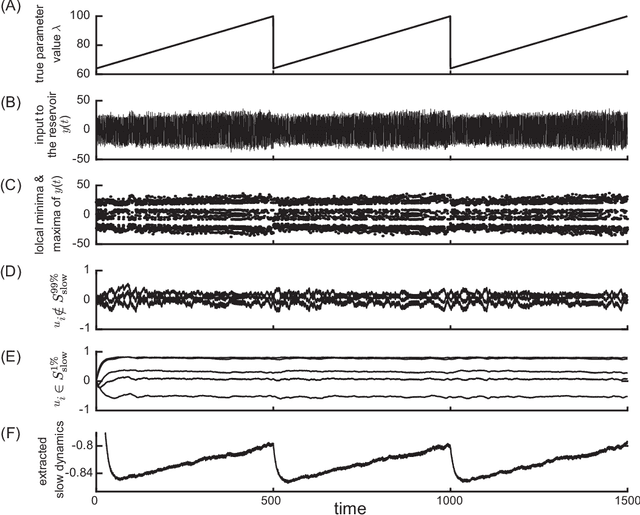
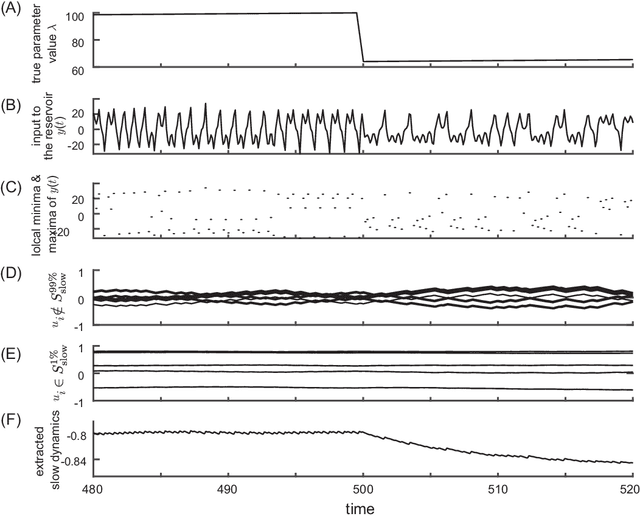
Nonlinear and non-stationary processes are prevalent in various natural and physical phenomena, where system dynamics can change qualitatively due to bifurcation phenomena. Traditional machine learning methods have advanced our ability to learn and predict such systems from observed time series data. However, predicting the behavior of systems with temporal parameter variations without knowledge of true parameter values remains a significant challenge. This study leverages the reservoir computing framework to address this problem by unsupervised extraction of slowly varying system parameters from time series data. We propose a model architecture consisting of a slow reservoir with long timescale internal dynamics and a fast reservoir with short timescale dynamics. The slow reservoir extracts the temporal variation of system parameters, which are then used to predict unknown bifurcations in the fast dynamics. Through experiments using data generated from chaotic dynamical systems, we demonstrate the ability to predict bifurcations not present in the training data. Our approach shows potential for applications in fields such as neuroscience, material science, and weather prediction, where slow dynamics influencing qualitative changes are often unobservable.

Biological neurons act as generalization filters in reservoir computing

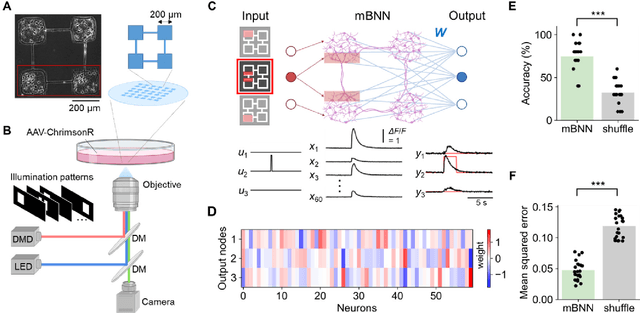
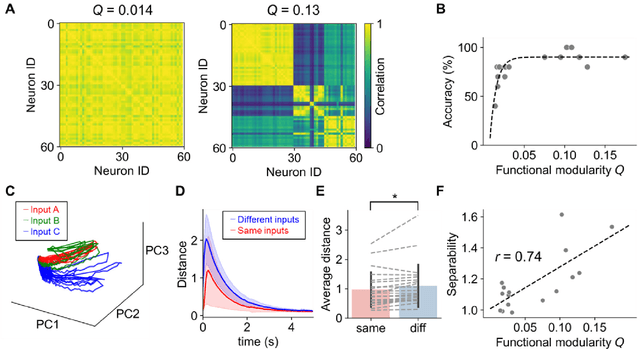
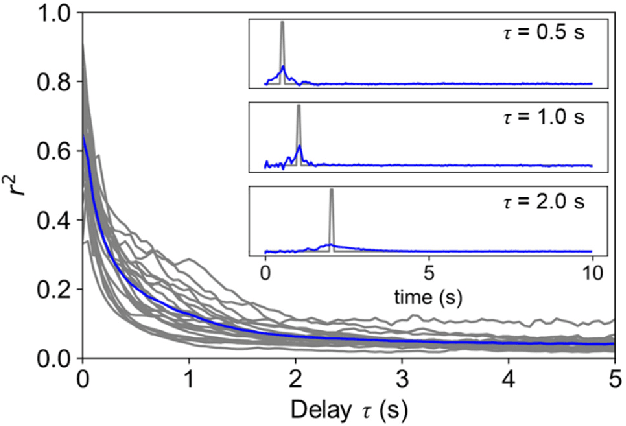
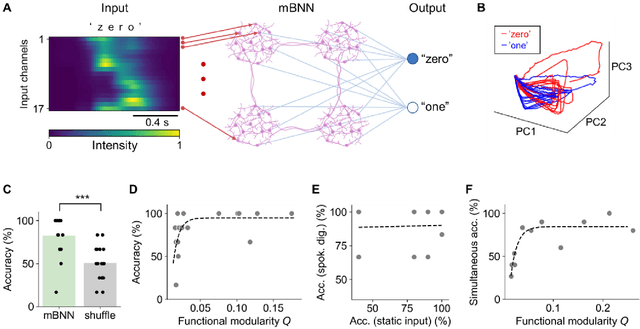
Reservoir computing is a machine learning paradigm that transforms the transient dynamics of high-dimensional nonlinear systems for processing time-series data. Although reservoir computing was initially proposed to model information processing in the mammalian cortex, it remains unclear how the non-random network architecture, such as the modular architecture, in the cortex integrates with the biophysics of living neurons to characterize the function of biological neuronal networks (BNNs). Here, we used optogenetics and fluorescent calcium imaging to record the multicellular responses of cultured BNNs and employed the reservoir computing framework to decode their computational capabilities. Micropatterned substrates were used to embed the modular architecture in the BNNs. We first show that modular BNNs can be used to classify static input patterns with a linear decoder and that the modularity of the BNNs positively correlates with the classification accuracy. We then used a timer task to verify that BNNs possess a short-term memory of ~1 s and finally show that this property can be exploited for spoken digit classification. Interestingly, BNN-based reservoirs allow transfer learning, wherein a network trained on one dataset can be used to classify separate datasets of the same category. Such classification was not possible when the input patterns were directly decoded by a linear decoder, suggesting that BNNs act as a generalization filter to improve reservoir computing performance. Our findings pave the way toward a mechanistic understanding of information processing within BNNs and, simultaneously, build future expectations toward the realization of physical reservoir computing systems based on BNNs.

Chaos may enhance expressivity in cerebellar granular layer

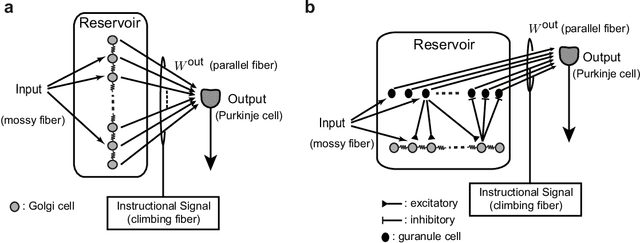
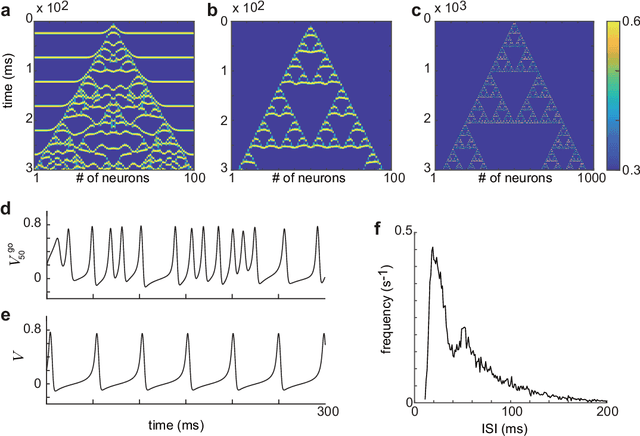
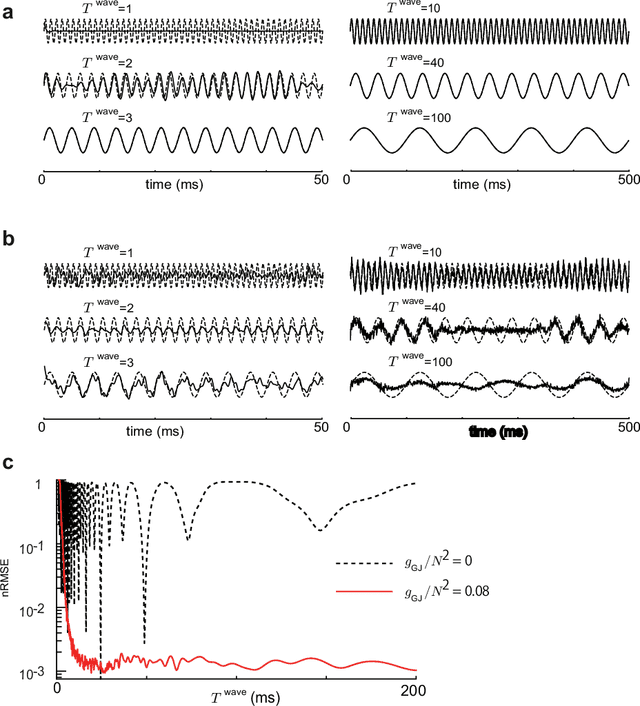
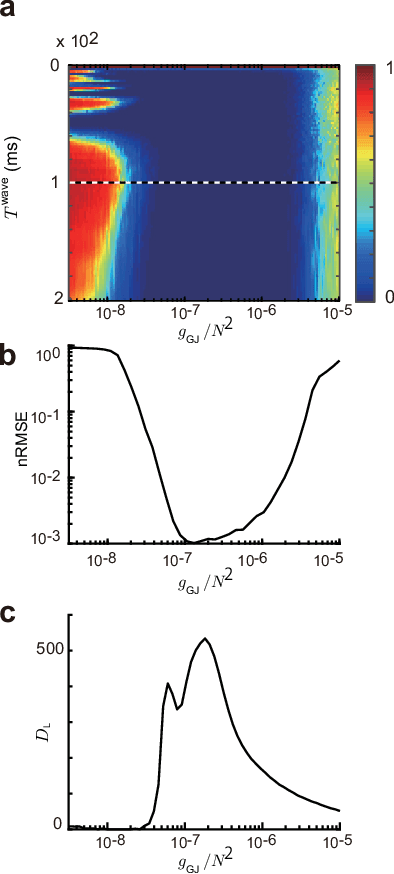
Recent evidence suggests that Golgi cells in the cerebellar granular layer are densely connected to each other with massive gap junctions. Here, we propose that the massive gap junctions between the Golgi cells contribute to the representational complexity of the granular layer of the cerebellum by inducing chaotic dynamics. We construct a model of cerebellar granular layer with diffusion coupling through gap junctions between the Golgi cells, and evaluate the representational capability of the network with the reservoir computing framework. First, we show that the chaotic dynamics induced by diffusion coupling results in complex output patterns containing a wide range of frequency components. Second, the long non-recursive time series of the reservoir represents the passage of time from an external input. These properties of the reservoir enable mapping different spatial inputs into different temporal patterns.