Prediction of Unobserved Bifurcation by Unsupervised Extraction of Slowly Time-Varying System Parameter Dynamics from Time Series Using Reservoir Computing

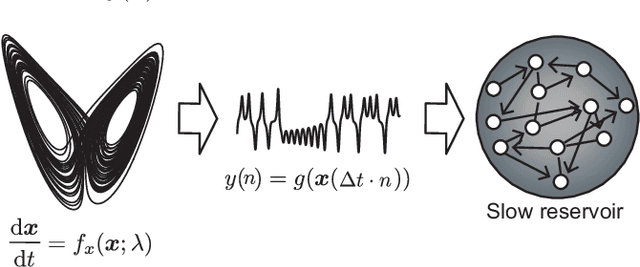
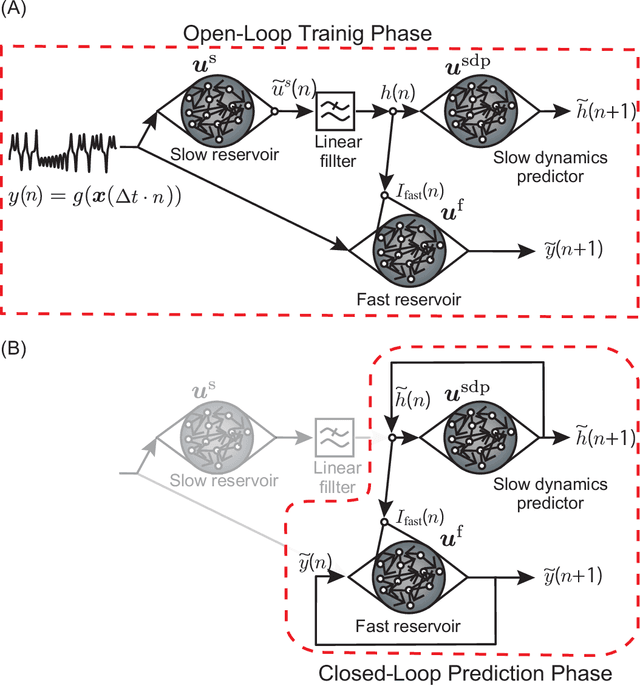
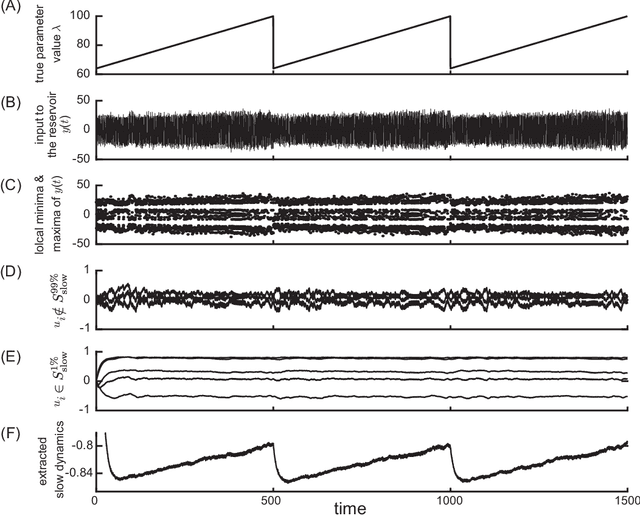
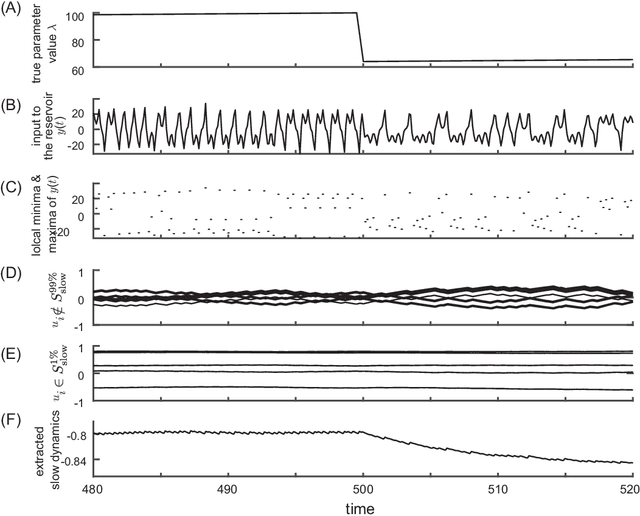
Nonlinear and non-stationary processes are prevalent in various natural and physical phenomena, where system dynamics can change qualitatively due to bifurcation phenomena. Traditional machine learning methods have advanced our ability to learn and predict such systems from observed time series data. However, predicting the behavior of systems with temporal parameter variations without knowledge of true parameter values remains a significant challenge. This study leverages the reservoir computing framework to address this problem by unsupervised extraction of slowly varying system parameters from time series data. We propose a model architecture consisting of a slow reservoir with long timescale internal dynamics and a fast reservoir with short timescale dynamics. The slow reservoir extracts the temporal variation of system parameters, which are then used to predict unknown bifurcations in the fast dynamics. Through experiments using data generated from chaotic dynamical systems, we demonstrate the ability to predict bifurcations not present in the training data. Our approach shows potential for applications in fields such as neuroscience, material science, and weather prediction, where slow dynamics influencing qualitative changes are often unobservable.

Chaos may enhance expressivity in cerebellar granular layer

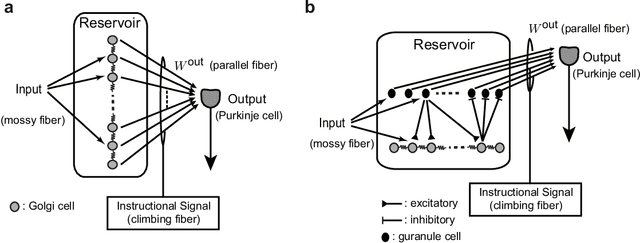
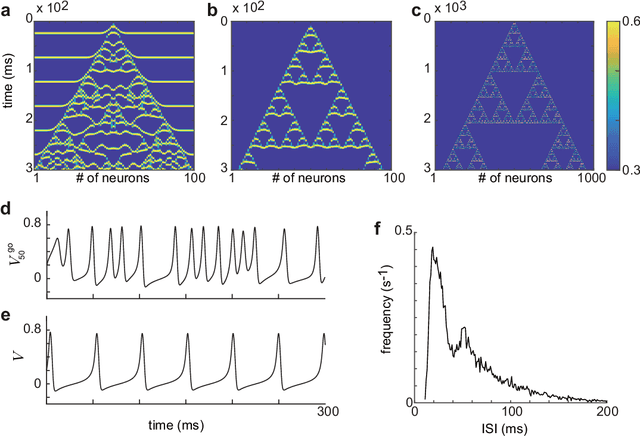
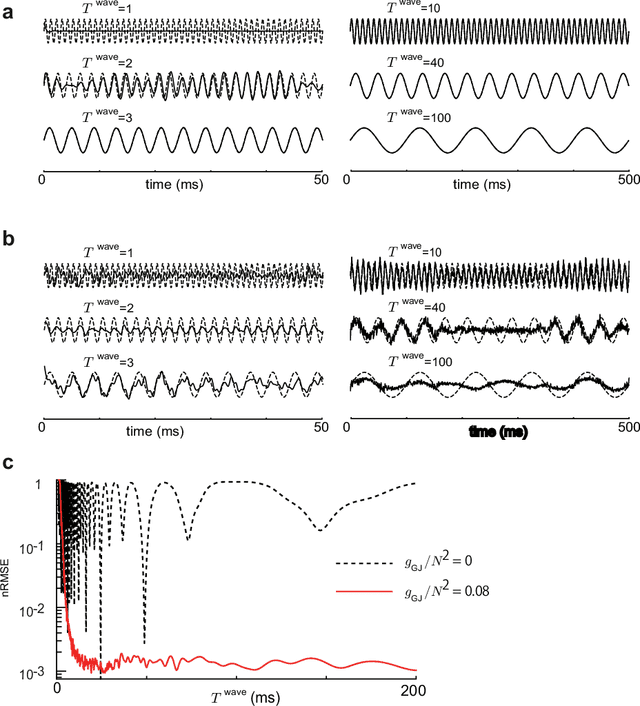
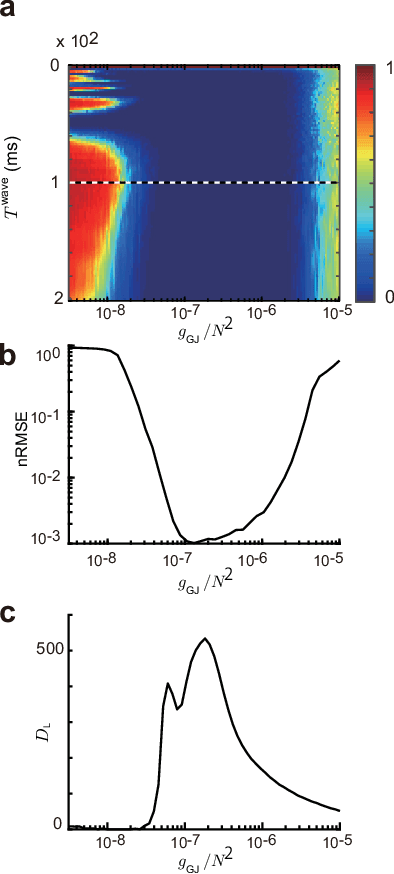
Recent evidence suggests that Golgi cells in the cerebellar granular layer are densely connected to each other with massive gap junctions. Here, we propose that the massive gap junctions between the Golgi cells contribute to the representational complexity of the granular layer of the cerebellum by inducing chaotic dynamics. We construct a model of cerebellar granular layer with diffusion coupling through gap junctions between the Golgi cells, and evaluate the representational capability of the network with the reservoir computing framework. First, we show that the chaotic dynamics induced by diffusion coupling results in complex output patterns containing a wide range of frequency components. Second, the long non-recursive time series of the reservoir represents the passage of time from an external input. These properties of the reservoir enable mapping different spatial inputs into different temporal patterns.