Chaos may enhance expressivity in cerebellar granular layer
Paper and Code
Jun 20, 2020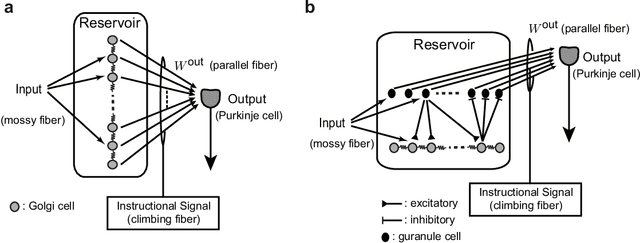
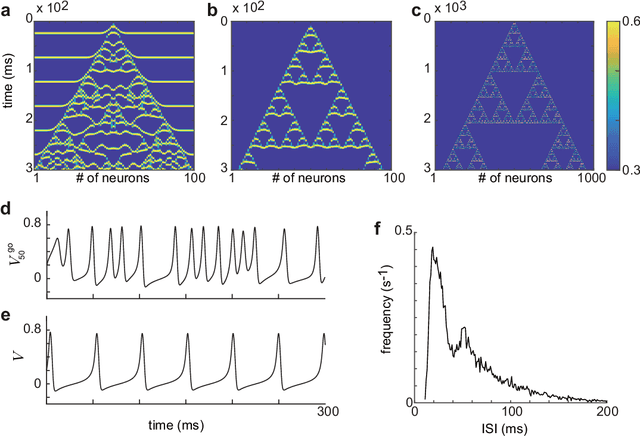
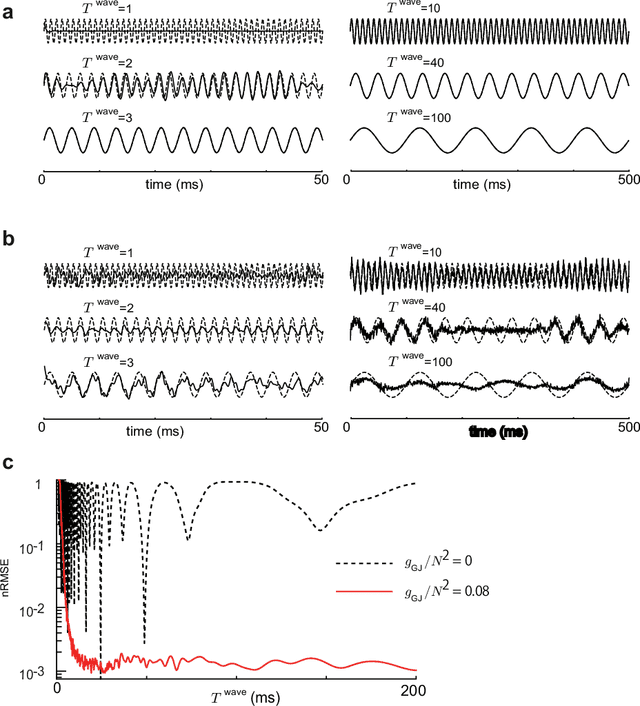
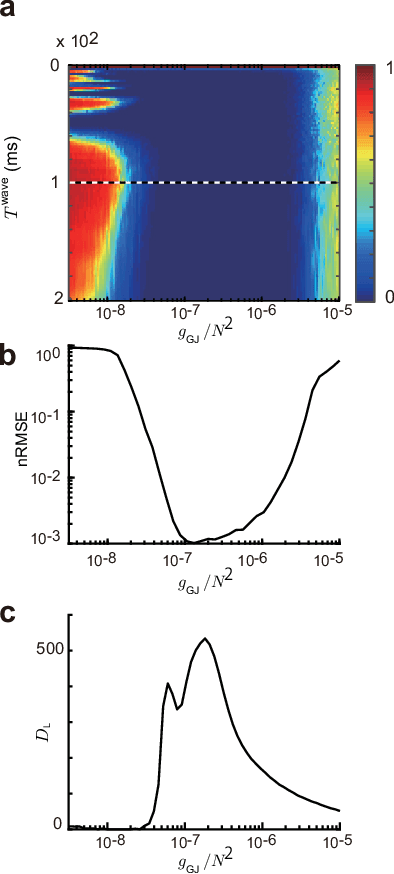
Recent evidence suggests that Golgi cells in the cerebellar granular layer are densely connected to each other with massive gap junctions. Here, we propose that the massive gap junctions between the Golgi cells contribute to the representational complexity of the granular layer of the cerebellum by inducing chaotic dynamics. We construct a model of cerebellar granular layer with diffusion coupling through gap junctions between the Golgi cells, and evaluate the representational capability of the network with the reservoir computing framework. First, we show that the chaotic dynamics induced by diffusion coupling results in complex output patterns containing a wide range of frequency components. Second, the long non-recursive time series of the reservoir represents the passage of time from an external input. These properties of the reservoir enable mapping different spatial inputs into different temporal patterns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge