Yufei zha
Push for Quantization: Deep Fisher Hashing
Aug 31, 2019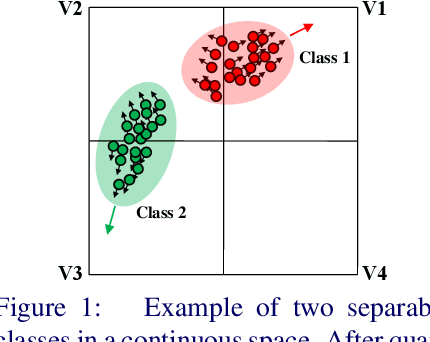
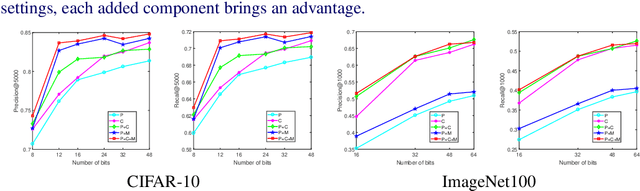
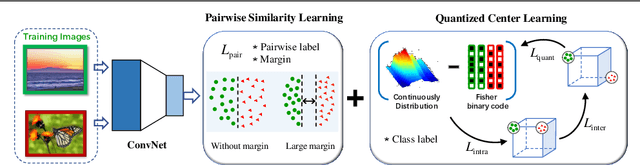
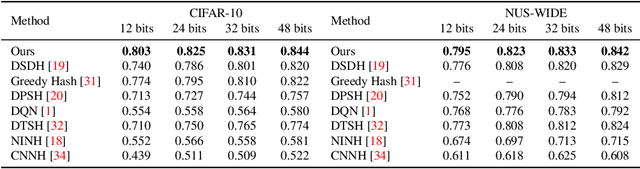
Abstract:Current massive datasets demand light-weight access for analysis. Discrete hashing methods are thus beneficial because they map high-dimensional data to compact binary codes that are efficient to store and process, while preserving semantic similarity. To optimize powerful deep learning methods for image hashing, gradient-based methods are required. Binary codes, however, are discrete and thus have no continuous derivatives. Relaxing the problem by solving it in a continuous space and then quantizing the solution is not guaranteed to yield separable binary codes. The quantization needs to be included in the optimization. In this paper we push for quantization: We optimize maximum class separability in the binary space. We introduce a margin on distances between dissimilar image pairs as measured in the binary space. In addition to pair-wise distances, we draw inspiration from Fisher's Linear Discriminant Analysis (Fisher LDA) to maximize the binary distances between classes and at the same time minimize the binary distance of images within the same class. Experiments on CIFAR-10, NUS-WIDE and ImageNet100 demonstrate compact codes comparing favorably to the current state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge