Yuening Zhang
Adaptation and Communication in Human-Robot Teaming to Handle Discrepancies in Agents' Beliefs about Plans
Jul 07, 2023



Abstract:When agents collaborate on a task, it is important that they have some shared mental model of the task routines -- the set of feasible plans towards achieving the goals. However, in reality, situations often arise that such a shared mental model cannot be guaranteed, such as in ad-hoc teams where agents may follow different conventions or when contingent constraints arise that only some agents are aware of. Previous work on human-robot teaming has assumed that the team has a set of shared routines, which breaks down in these situations. In this work, we leverage epistemic logic to enable agents to understand the discrepancy in each other's beliefs about feasible plans and dynamically plan their actions to adapt or communicate to resolve the discrepancy. We propose a formalism that extends conditional doxastic logic to describe knowledge bases in order to explicitly represent agents' nested beliefs on the feasible plans and state of execution. We provide an online execution algorithm based on Monte Carlo Tree Search for the agent to plan its action, including communication actions to explain the feasibility of plans, announce intent, and ask questions. Finally, we evaluate the success rate and scalability of the algorithm and show that our agent is better equipped to work in teams without the guarantee of a shared mental model.
Generalized Conflict-directed Search for Optimal Ordering Problems
Mar 31, 2021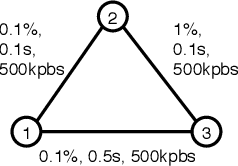
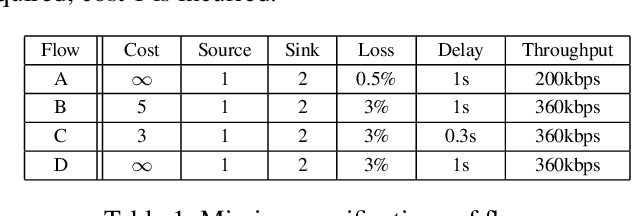
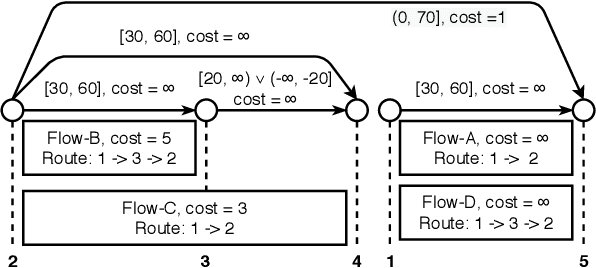

Abstract:Solving planning and scheduling problems for multiple tasks with highly coupled state and temporal constraints is notoriously challenging. An appealing approach to effectively decouple the problem is to judiciously order the events such that decisions can be made over sequences of tasks. As many problems encountered in practice are over-constrained, we must instead find relaxed solutions in which certain requirements are dropped. This motivates a formulation of optimality with respect to the costs of relaxing constraints and the problem of finding an optimal ordering under which this relaxing cost is minimum. In this paper, we present Generalized Conflict-directed Ordering (GCDO), a branch-and-bound ordering method that generates an optimal total order of events by leveraging the generalized conflicts of both inconsistency and suboptimality from sub-solvers for cost estimation and solution space pruning. Due to its ability to reason over generalized conflicts, GCDO is much more efficient in finding high-quality total orders than the previous conflict-directed approach CDITO. We demonstrate this by benchmarking on temporal network configuration problems, which involves managing networks over time and makes necessary tradeoffs between network flows against CDITO and Mixed Integer-Linear Programing (MILP). Our algorithm is able to solve two orders of magnitude more benchmark problems to optimality and twice the problems compared to CDITO and MILP within a runtime limit, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge