Generalized Conflict-directed Search for Optimal Ordering Problems
Paper and Code
Mar 31, 2021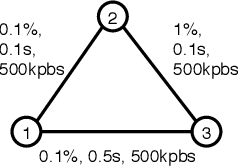
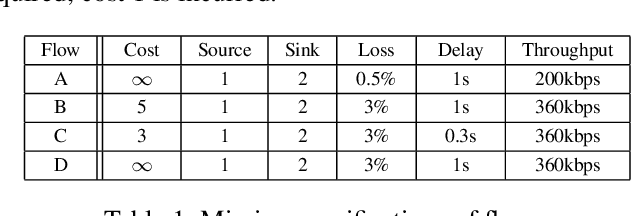
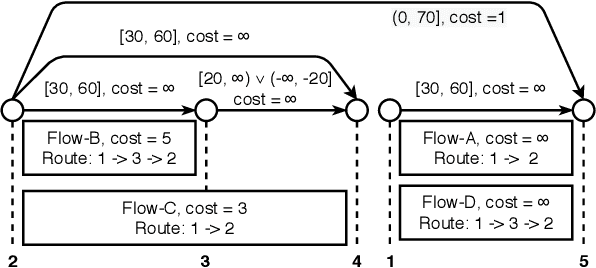

Solving planning and scheduling problems for multiple tasks with highly coupled state and temporal constraints is notoriously challenging. An appealing approach to effectively decouple the problem is to judiciously order the events such that decisions can be made over sequences of tasks. As many problems encountered in practice are over-constrained, we must instead find relaxed solutions in which certain requirements are dropped. This motivates a formulation of optimality with respect to the costs of relaxing constraints and the problem of finding an optimal ordering under which this relaxing cost is minimum. In this paper, we present Generalized Conflict-directed Ordering (GCDO), a branch-and-bound ordering method that generates an optimal total order of events by leveraging the generalized conflicts of both inconsistency and suboptimality from sub-solvers for cost estimation and solution space pruning. Due to its ability to reason over generalized conflicts, GCDO is much more efficient in finding high-quality total orders than the previous conflict-directed approach CDITO. We demonstrate this by benchmarking on temporal network configuration problems, which involves managing networks over time and makes necessary tradeoffs between network flows against CDITO and Mixed Integer-Linear Programing (MILP). Our algorithm is able to solve two orders of magnitude more benchmark problems to optimality and twice the problems compared to CDITO and MILP within a runtime limit, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge