Constant Directivity Loudspeaker Beamforming

Loudspeaker array beamforming is a common signal processing technique for acoustic directivity control and robust audio reproduction. Unlike their microphone counterpart, loudspeaker constraints are often heterogeneous due to arrayed transducers with varying operating ranges in frequency, acoustic-electrical sensitivity, efficiency, and directivity. This work proposes a frequency-regularization method for generalized Rayleigh quotient directivity specifications and two novel beamformer designs that optimize for maximum efficiency constant directivity (MECD) and maximum sensitivity constant directivity (MSCD). We derive fast converging and analytic solutions from their quadratic equality constrained quadratic program formulations. Experiments optimize generalized directivity index constrained beamformer designs for a full-band heterogeneous array.

Gaussian Process Models for HRTF based Sound-Source Localization and Active-Learning

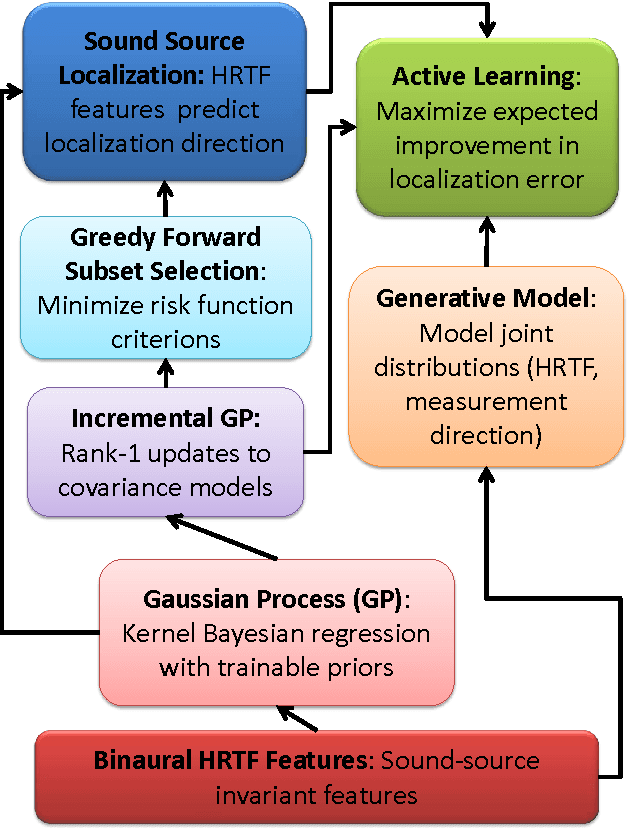
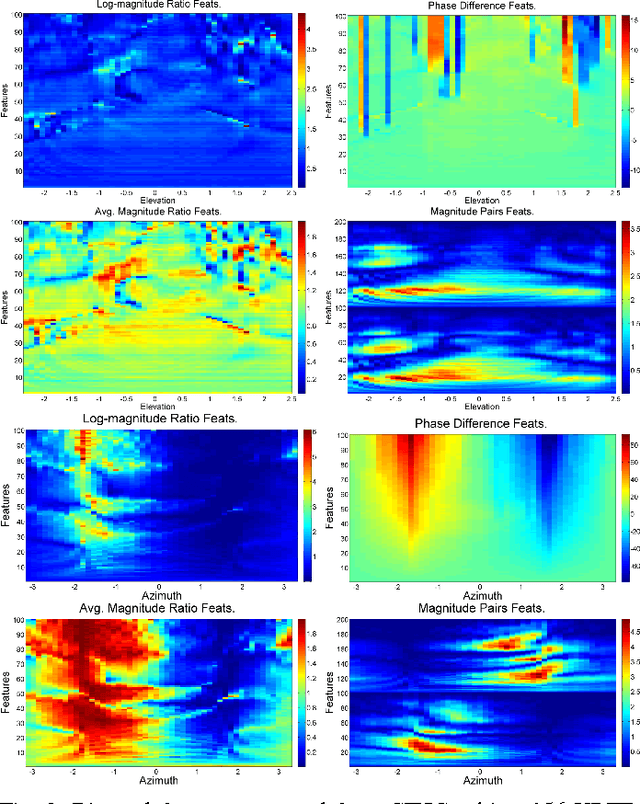
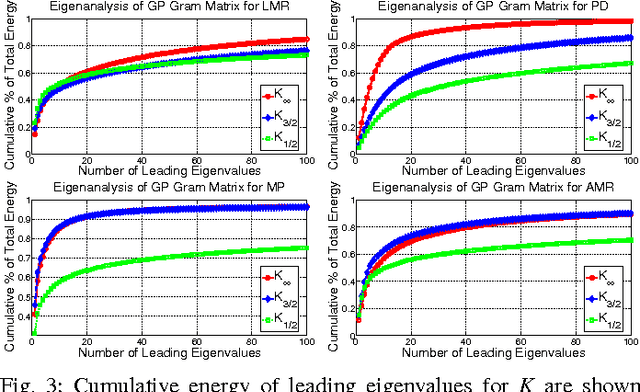
From a machine learning perspective, the human ability localize sounds can be modeled as a non-parametric and non-linear regression problem between binaural spectral features of sound received at the ears (input) and their sound-source directions (output). The input features can be summarized in terms of the individual's head-related transfer functions (HRTFs) which measure the spectral response between the listener's eardrum and an external point in $3$D. Based on these viewpoints, two related problems are considered: how can one achieve an optimal sampling of measurements for training sound-source localization (SSL) models, and how can SSL models be used to infer the subject's HRTFs in listening tests. First, we develop a class of binaural SSL models based on Gaussian process regression and solve a \emph{forward selection} problem that finds a subset of input-output samples that best generalize to all SSL directions. Second, we use an \emph{active-learning} approach that updates an online SSL model for inferring the subject's SSL errors via headphones and a graphical user interface. Experiments show that only a small fraction of HRTFs are required for $5^{\circ}$ localization accuracy and that the learned HRTFs are localized closer to their intended directions than non-individualized HRTFs.